Research Projects

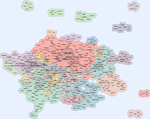
	GMap is an algorithm for visualizing graphs as maps; the GMap visualization system is fully functional online. Information visualization can be invaluable in making sense out of large data sets. However, traditional graph visualization methods often fail to capture the underlying structural information, clustering, and neighborhoods. GMap, provides a way to overcome some of the shortcomings with the help of the geographic map metaphor. While graphs, charts, and tables often require considerable effort to comprehend, a map representation is more intuitive, as most people are very familiar with maps and even enjoy carefully examining maps. The effectiveness of GMap is illustrated with examples from several domains, namely TV shows, Amazon books, and last.fm music. The last map led to over 630K views on a stumbleuppon.
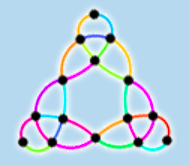
	Lombardi is a new force-directed spring embedder for graph drawing, inspired by the style of the American artist Mark Lombardi. The main features that set our Lombardi spring embedder apart from other approaches are that straight edges are replaced by circular arcs, and that the arcs around each vertex are evenly spaced out. The objectives of this approach are to improve readability and aesthetic appeal of graph drawings. Initial user feedback strongly indicates the aesthetic appeal of this style of drawing, with some associated keywords being “more natural”, “balloon animals”, “blobby”, “cute and cuddly." A picture gallery and movie gallery illustrates the approach.
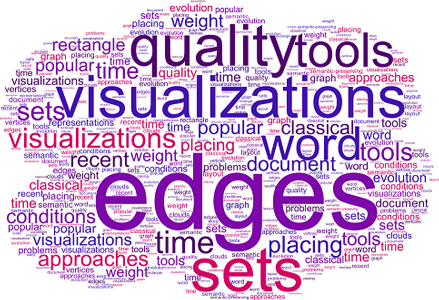
	Semantic Word Clouds: A word cloud consists of the most important words in a text document. In a semantic-preserving word cloud, related words are placed close to each other. Words are scaled by a factor roughly proportional to their importance. The clouds can be modified with various fonts, layouts, and color schemes.
	Maps of Computer Science: The MOCS project provides a method to visualize concept maps of topics from the DBLP database of computer science research papers. We use the titles of papers in the database to extract prominent words and phrases and calculate their similarity based on cooccurrence in titles. These terms are clustered and laid out based on their similarity values, providing a visual representation of topic space. Heatmap overlays allow us to visualize the profile of a time frame, conference, journal, or author over the base map. Also, different base maps can be created: maps that are representative samples of all papers available in DBLP, or maps limited to specific time frames, conferences, journals, or authors. MOCS makes topic maps of the field, heatmaps of various conferences (e.g., STOC), journals over time (e.g., JACM first decade vs last decade), as well as researchers and groups.
	Citizen Scientists for Trajectory Analysis: We study the use of games and crowd sourcing to capture and analyze scientific trajectory data. We design games to employ citizen scientists to trace (i) static objects in images and (ii) moving objects such as ants or bees in video data. We study the challenging data validation problem of selecting for each object, one accurate trajectory from the several (possibly inaccurate) trajectories which are submitted by the citizen scientists playing our game. For numerical values finding the consensus of several estimates is easily done by taking an average . Computing the consensus of traces is not as straight forward. We design algorithm which use clustering, geometric alignment, sampling, as well as other methods for this purpose.
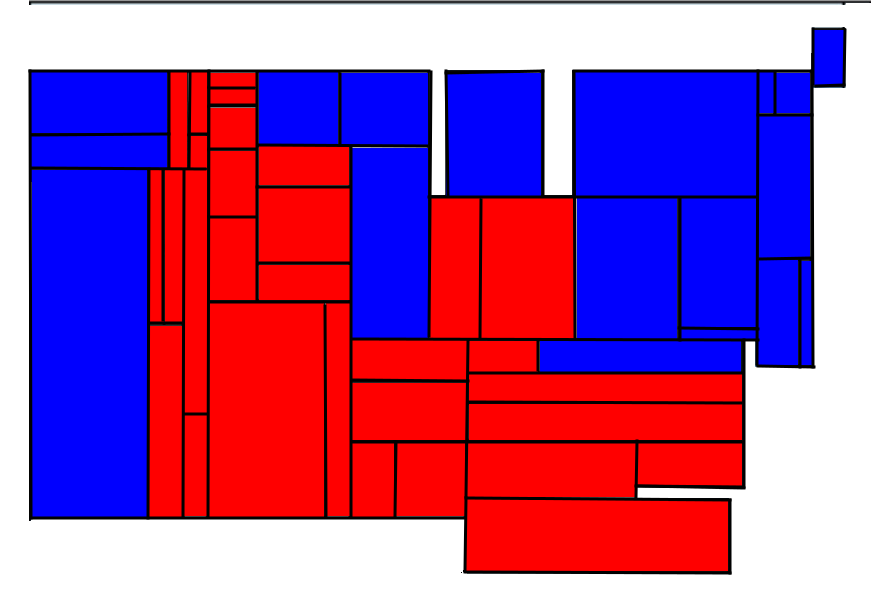
	Algorithms for Cartogram Computations: Cartograms are used for visualizing geographically distributed data by scaling the regions of a map (e.g., countries in Europe) such that their areas are proportional to the data associated with them (e.g., GDP). Thus the cartogram computation problem can be thought of as a map deformation problem where the input is a planar polygonal map and an assignment of some positive weight for each region. The goal is to create a deformed map where the area of each region realizes the weight assigned to it (no cartographic error) while the overall map remains recognizable (e.g., the topology, the relative positions and the shapes of the regions remain the same). Since achieving no cartographic error and preserving map readability are impossible to achieve simultaneously, all the cartogram generation algorithms tolerate some error in one or both of these criteria. We define some quantitative measures that can be used to evaluate how faithfully a cartogram represents the weights, as well as several measures for evaluating the readability of the final representation. We then study several early algorithms for computing cartograms and two new ones and compare them in terms of our quantitative measures.
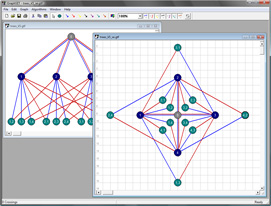
	GraphSET is our Graph Simultaneous Embedding Tool. We developed this software in order to have a pracatical way to study several types of problems in simultaneous graph embeddings: simultaneous geometric embedding, simultaneous embedding with fixed edges, and colored simultaneous embedding. GraphSET can be used to study theoretical problems in simultaneous graph drawing and to produce drawings from known algorithms for these problems. The software and the code are available for download together with a user guide, screenshots, and simultaneous embedding challenges.
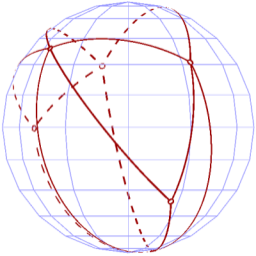
	SMorph: Spherical Graph Morphing SMorph is a project that deals with morphing of graph drawings on the surface of the sphere. We are interested in the problem of intersection-planar graph morphing, and in particular, a generalization from Euclidian space to spherical space. We show that under certain conditions, there exists a continuous and intersection-free morph between two sphere drawings of a maximally planar graph, where sphere drawings are the spherical equivalent of plane drawings: crossings-free geodesic-arc drawings. In addition to the existence proof, we describe a morphing algorithm along with its implementation.
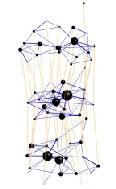
	GRIP: Graph Drawing with Intelligent Placement GRIP is designed for drawing large graphs and uses a novel multi-dimensional force-directed method together with fast energy function minimization. The algorithm underlying the system employs a simple recursive coarsening scheme. Rather than being placed at random, vertices are placed intelligently, several at a time, at locations close to their final positions. The running time and space complexity of the system are near linear. The implementation is in C using OpenGL for 3D viewing. GRIP allows for drawing graphs with tens of thousands of vertices in under one minute on a mid-range PC. To the best of the authors' knowledge, GRIP surpasses the fastest previous algorithms. However, speed is not achieved at the expense of quality as the resulting drawings are quite aesthetically pleasing. For a sample of what GRIP does, take a look a few animated examples.
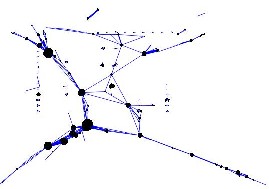
	TGRIP: Temporal Graph Drawing TGRIP is an application designed for interactive visualization of large weighted graphs that have a temporal component. TGRIP is designed for drawing large graphs and uses a novel multi-dimensional force-directed method together with fast energy function minimization. The algorithm underlying the system employs a simple recursive coarsening scheme. Rather than being placed at random, vertices are placed intelligently, several at a time, at locations close to their final positions. In most applications it is necessary to be able to visualize graphs in which vertices/edges have weights. The layout component should take into account these weights while doing the placement. A pair of vertices connected with a large weighted edge should be placed closer to each other than another pair with smaller edge weight for example. TGRIP handles this by introducing the weight concept to the general force-directed method. The graphs that we are interested in evolve through time. The changes in the graph include adding and removing vertices/edges. TGRIP allows us to control the tradeoff between readable drawings and mental map preservation between consecutive drawings. Finally, the system generates smooth animations between consecutive time steps.
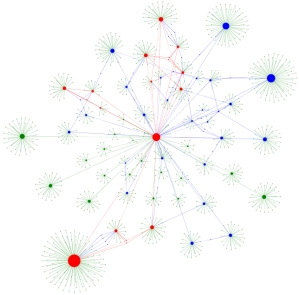
	GraphAEL: Graph Animations with Evolving Layouts GraphAEL extracts three types of evolving graphs from the Graph Drawing literature and creates 2D and 3D animations of the evolutions. We study citation graphs, topic graphs, and collaboration graphs. We also create different graphs which capture the nature of change between two given time periods.
	graphael graphael is a system that implements several classic force-directed layout methods, as well as several novel layout methods for non-Euclidean geometries, including hyperbolic and spherical. The system can handle large graphs, using multi-scale variations of the force-directed methods. Finally, the system can layout and visualize graphs that evolve though time, using static views, animation, and morphing. The current system is equipped with a core package of force-directed algorithms and visualization tools. In addition to putting together well-known algorithms and visualization methods, graphael contains several novel features. Some of these features include support for temporal graphs, interactive graph visualization, multi-scale layout algorithms for large graphs, and embedding graphs in non-Euclidean spaces, such as hyperbolic space and spherical space.
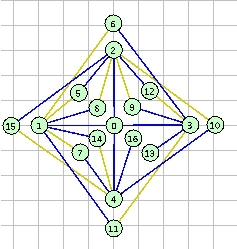
	TetraTetris TetraTetris is a multi-user game utilizing a DiamondTouch table. The DiamondTouch table is a touch-sensitive input device that allows several users to interact with a program at the same time and do so using their hands. We describe our exploration of the capabilities and limitations of the DiamondTouch by focusing on TetraTetris, one of the first nontrivial applications written specifcally for the DiamondTouch hardware. TetraTetris is a multi-player game, loosely based on the popular game Tetris, in which players use their hands to manipulate objects moving around on the table; it illustrates some of the table's key advantages and drawbacks by comparison with conventional input hardware. In this paper we describe the DiamondTouch hardware, the rules of TetraTetris, the problems we encountered implementing it, and what TetraTetris can show us about the future of input devices like the table.
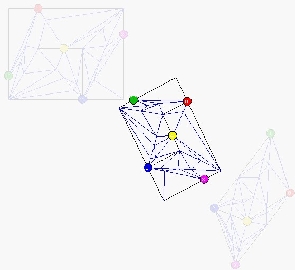
	Simultaneous Embedding Simultaneous Embedding is a new graph theoretical problem. This project deals with the simultaneous embedding of multiple planar graphs. The goal is to produce aesthetically pleasing drawings for the two graphs by means of a heuristic algorithm and with human assistance. Our implementation uses the DiamondTouch table, a multi- user, touch-sensitive input device, to take advantage of direct physical interaction of several users working collaboratively. The system can be downloaded or the corresponding applet can be used online.
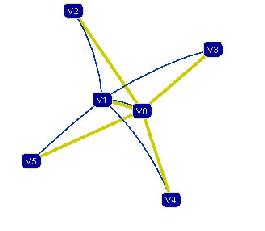
	GMorph: Intersection Free Morphing of Planar Graphs GMorph is an implementation of an algorithm for morphing of planar graphs. Morphing refers to the process of transforming one shape (the source) into another (the target) In planar graph morphing we would like to transform a given source graph to another pre-specified target graph. A smooth transformation of one graph into another can be useful for numerous problems from graph drawing. In particular, when dealing with dynamic graphs and graphs that change through time, it is crucial to preserve the mental map of the user. Thus, it is important to minimize the changes to the drawing and to create a smooth transition between consecutive drawings. Another important goal is to avoid creating any intersections throughout the morph. We designed and implemented an algorithm that can morph between drawings with straight-line segments, bends and it relies on a combination of techniques to achieve smooth transformations: rigid morphing, compatible triangulations, as well as morphing based on interpolation of the convex representations of the graphs. Here is a short (5 min) but large (200MB+) video overview of the project.
	SIMG: Simultaneous Graph Drawing Consider the problem of drawing and displaying a series of related graphs that share all or parts of the same vertex set. The graphs may represent different relations between the same set of objects. SIMG illustrates different approaches to simultaneous graph drawing. We have developed and implemented three different techniques for laying out a series of graphs to be simultaneously embedded. We have also designed and implemented three different schemes for visualizing multiple graphs. While each of these visualization schemes corresponds closely to one of our layout algorithms, any combination of a layout algorithm and a visualization scheme can be used. When visualizing a series of graphs that share all or parts of the same vertex set, it is important to display the graphs in such a way that the user can either focus on one graph at a time without being confused by the other graphs in the series or visualize the layouts of multiple graphs at the same time to get a mental map between the different relations represented by each graph.
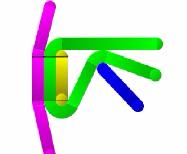	Fat-Edges Graph Drawing Traditionally, graph drawing algorithms represent vertices as circles and edges as closed curves connecting the vertices. In this paper we consider the problem of drawing graphs with edges of variable thickness. The thickness of an edge is often used as a visualization cue, to indicate importance, or to convey some additional information. We present a model for drawing with fat edges and a corresponding polynomial time algorithm that uses the model. A short movie and paper illustrate the algorithm.
	SPLaT: Self-Plagiarism Tool SPLat is a tool for self-plagiarism detection. The current version of SPlaT functions as a web spider that crawls through the web sites of fifty Computer Science departments, downloading research papers to search for instances of self-plagiarism by Computer Science academics. Instances of self-plagiarism for each author are reported so that they may be investigated in order to determine if they are truly fraudulent papers.