CSc 372 - Comparative Programming Languages
12 : Haskell -- Composing Functions
Christian Collberg
Department of Computer Science
University of Arizona
We want to discover frequently
occurring patterns of computation. These patterns
are then made into (often higher-order) functions
which can be specialized and combined.
map f L and filter f L can be specialized
and combined:
![\begin{gprogram}
double :: [Int] -> [Int]\\
double xs = map ((*) 2) xs\\
\\
p...
...) xs) \\
\redtxt{? doublePos [2,3,0,-1,5]} \\
\mbox{[4, 6, 10]}
\end{gprogram}](img1.gif)
- Functional composition is a kind of ``glue'' that
is used to ``stick'' simple functions together
to make more powerful ones.
- In mathematics the ring symbol (
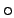 ) is used
to compose functions:
) is used
to compose functions:
- In Haskell we use the dot (".") symbol:
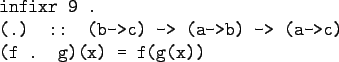
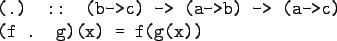
Composition
- "." takes two functions f and g as
arguments, and returns a new function h
as result.
- g is a function of type a->b.
- f is a function of type b->c.
- h is a function of type a->c.
- (f.g)(x) is the same as
z=g(x) followed by f(z).
- We use functional composition to write functions
more concisely. These definitions are equivalent:
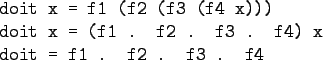
- The last form of doit is preferred.
doit's arguments are implicit;
it has the same parameters as the composition.
- doit can be used in higher-order
functions (the second form is preferred):
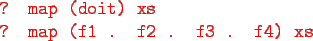
- Assume that we have a function fill that
splits a string into filled lines:
![\begin{gprogram}
fill :: string -> [string] \\
fill s = splitLines (splitWords s)
\end{gprogram}](img8.gif)
- fill first splits the string into
words (using splitWords) and
then into lines:
![\begin{gprogram}
splitWords :: string -> [word] \\
splitLines :: [word] -> [line]
\end{gprogram}](img9.gif)
- We can rewrite fill using function
composition:
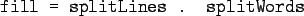
- "." is right associative. I.e.
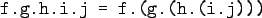
- "." has higher precedence (binding power)
than any other operator, except function application:
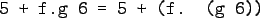
- "." is associative:
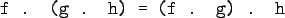
- "id" is "."'s identity element,
i.e id . f = f = f . id:
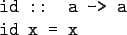
- Define a function count which counts the
number of lists of length
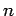 in a list
in a list 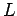 :
:
![\begin{gprogram}
\xx count 2 [[1],[],[2,3],[4,5],[]] $\Rightarrow$ 2
\end{gprogram}](img17.gif)
Using recursion:
![\begin{gprogram}
count :: Int -> [[a]] -> Int \\
count \_ [] = 0 \\
count n (x...
...xxxx = 1 + count n xs \\
\x \vert otherwise \xxxxxx = count n xs
\end{gprogram}](img18.gif)
Using functional composition:
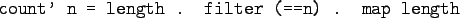
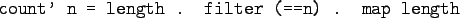
Count
- Note that
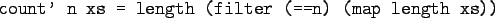
- last returns the last element of a list.
- init returns everything but
the last element of a list.
Definitions:

Simulations:
![\begin{gprogram}
{[1,2,3]}$\stackrel{\tc{reverse}}{\Longrightarrow}$[3,2,1]$\sta...
...ightarrow}$
[2,1]$\stackrel{\tc{reverse}}{\Longrightarrow}$[1,2]
\end{gprogram}](img22.gif)
- any p xs returns True
if p x == True for some
x in xs:
![\begin{gprogram}
any ((==)0) [1,2,3,0,5] $\Rightarrow$ True \\
any ((==)0) [1,2,3,4] $\Rightarrow$ False
\end{gprogram}](img23.gif)
Using recursion:
![\begin{gprogram}
any :: (a -> Bool) -> [a] -> Bool \\
any \_ [] = False \\
any p (x:xs) = \= \vert p x = True \\
\x \vert otherwise = any p xs
\end{gprogram}](img24.gif)
Using composition:
![\begin{gprogram}
any p = or . map p \\
\redtxt{{[1,0,3]}$\stackrel{\tc{map ((==...
...dtxt{[False,True,False]$\stackrel{\tc{or}}{\Longrightarrow}$True}
\end{gprogram}](img25.gif)
- Let's have another look at one simple (!) function,
commaint.
- commaint works on strings, which are simply
lists of characters.
- You are not
 now supposed to understand this!
now supposed to understand this!
From the commaint documentation:
[commaint] takes a single string argument
containing a sequence of digits, and outputs the
same sequence with commas inserted after every
group of three digits, 
Sample interaction:
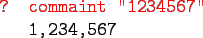
commaint in Haskell:

CommaInt

- iterate (drop 3) s returns the infinite list of strings
![\begin{gprogram}[s, drop 3 s, drop 3 (drop 3 s),\\
\x drop 3 (drop 3 (drop 3 s)), $\cdots$]
\end{gprogram}](img30.gif)
- map (take n) xss shortens the lists in xss
to n elements.

- takeWhile (not.null) removes all empty strings from
a list of strings.
- foldr1 (
 x y->x++","++y) s takes a list
of strings s as input. It appends the strings
together, inserting a comma in between each pair of strings.
x y->x++","++y) s takes a list
of strings s as input. It appends the strings
together, inserting a comma in between each pair of strings.
- (
 x y->x++","++y)
is called a lambda expression.
x y->x++","++y)
is called a lambda expression.
- Lambda expressions are simply a way of writing
(short) functions inline. Syntax:
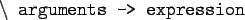
- Thus, commaint could just as well have been
written as
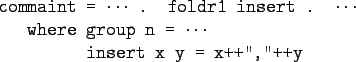
Examples:
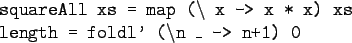
- The built-in operator "."
(pronounced ``compose'') takes
two functions f and g as argument, and
returns a new function h as result.
- The new function h = f . g combines
the behavior of f and g: applying h
to an argument a is the same
as first applying g to a, and then
applying f to this result.
- Operators can, of course, also be composed:
((+2) . (*3)) 3 will return 2 + (3 * 3) = 11.
- Write a function mid xs which returns
the list xs without its first and last element.
- use recursion
- use init, tail, and functional composition.
- use reverse, tail, and functional composition.
![\begin{gprogram}
\redtxt{? mid [1,2,3,4,5]} $\Rightarrow$ [2,3,4] \\
\redtxt{?...
...} $\Rightarrow$ ERROR \\
\redtxt{? mid [1,3]} $\Rightarrow$ []
\end{gprogram}](img35.gif)
Christian S. Collberg
2005-09-19
![\begin{gprogram}
double :: [Int] -> [Int]\\
double xs = map ((*) 2) xs\\
\\
p...
...) xs) \\
\redtxt{? doublePos [2,3,0,-1,5]} \\
\mbox{[4, 6, 10]}
\end{gprogram}](img1.gif)
![\begin{gprogram}
double :: [Int] -> [Int]\\
double xs = map ((*) 2) xs\\
\\
p...
...) xs) \\
\redtxt{? doublePos [2,3,0,-1,5]} \\
\mbox{[4, 6, 10]}
\end{gprogram}](img1.gif)
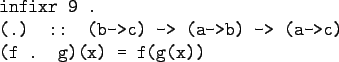
![]()
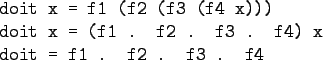
![]()
![\begin{gprogram}
count :: Int -> [[a]] -> Int \\
count \_ [] = 0 \\
count n (x...
...xxxx = 1 + count n xs \\
\x \vert otherwise \xxxxxx = count n xs
\end{gprogram}](img18.gif)
![]()
![]()

![\begin{gprogram}
{[1,2,3]}$\stackrel{\tc{reverse}}{\Longrightarrow}$[3,2,1]$\sta...
...ightarrow}$
[2,1]$\stackrel{\tc{reverse}}{\Longrightarrow}$[1,2]
\end{gprogram}](img22.gif)
![]()
![\begin{gprogram}
any :: (a -> Bool) -> [a] -> Bool \\
any \_ [] = False \\
any p (x:xs) = \= \vert p x = True \\
\x \vert otherwise = any p xs
\end{gprogram}](img24.gif)
![]()



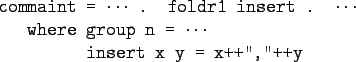
![]()
![\begin{gprogram}
\redtxt{? mid [1,2,3,4,5]} $\Rightarrow$ [2,3,4] \\
\redtxt{?...
...} $\Rightarrow$ ERROR \\
\redtxt{? mid [1,3]} $\Rightarrow$ []
\end{gprogram}](img35.gif)