In English, this reads:
``Generate a list where the elements are of the form expr, such that the elements fulfill the conditions in the qualifiers.''
Christian Collberg
Department of Computer Science
University of Arizona
``Generate a list where the elements are of the form expr, such that the elements fulfill the conditions in the qualifiers.''
![\begin{gprogram}
\mbox{[n \vert n<-[1..5]]} $\Rightarrow$\ [1,2,3,4,5] \\
\\
\...
...ox{[(n,n*n) \vert n<-[1..3]]} $\Rightarrow$\ [(1,1),(2,4),(3,9)]
\end{gprogram}](img3.gif)
![\begin{gprogram}
\mbox{[n*n \vert n<-[1..9],even n]} $\Rightarrow$\ [4,16,36,64]...
...ox{[(n,n*n) \vert n<-[1..3],n<n*n]} $\Rightarrow$\ [(2,4),(3,9)]
\end{gprogram}](img4.gif)
Pascal:
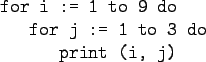
Haskell:
![\begin{gprogram}[(i,j) \vert i<-[1..9], j<-[1..3]] $\Rightarrow$\ \\
\xx [\x (1...
...(2,1),(2,2),(2,3),\\
\xxxx $\cdots$\ \\
\xxx (9,1),(9,2),(9,3)]
\end{gprogram}](img7.gif)
Pascal:
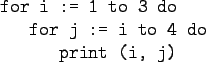
Haskell:
![\begin{gprogram}[(i,j) \vert i<-[1..3], j<-[i..4]] $\Rightarrow$\ \\
\xx [\x (1...
...x{[n*n \vert n<-[1..10], even n]} $\Rightarrow$\ [4,16,36,64,100]
\end{gprogram}](img9.gif)
In English:
``Generate a list of elements of the form 2*x, where the x:s are the positive elements from the list xs.
In Haskell:
![\begin{gprogram}
doublePos :: [Int] -> [Int] \\
doublePos xs = [2*x \vert x<-xs, x>0] \\
\\
\redtt{> doublePos [-1,-2,1,2,3]} \\
\x [2,4,6]
\end{gprogram}](img10.gif)
Example:
![]()
Haskell:
![]()
Examples:
![]()
In Haskell:
![]()
Pythagorean Triads:
![\begin{gprogram}
triads n = [(x,y,z)\vert \\
\x x<-[1..n], y<-[1..n], z<-[1..n]...
... == z\verb+^+2] \\
\\
triads 5 $\Rightarrow$\ [(3,4,5),(4,3,5)]
\end{gprogram}](img18.gif)
![\begin{gprogram}
triads' n = [(x,y,z)\vert \\
\x x<-[1..n], y<-[x..n], z<-[y..n...
...z\verb+^+2] \\
\\
triads' 11 $\Rightarrow$\ [(3,4,5), (6,8,10)]
\end{gprogram}](img19.gif)
Defining available (UK) coins:
![\begin{gprogram}
type Coin = Int \\
coins :: [Coin] \\
coins = reverse (sort [1,2,5,10,20,50,100])
\end{gprogram}](img20.gif)
Example:
![\begin{gprogram}
\redtt{> change 23} \\
\x [20,2,1] \\
\redtt{> coins} \\
\x ...
...> all\_change 4} \\
\x [[2,2],[2,1,1],[1,2,1],[1,1,2],[1,1,1,1]]
\end{gprogram}](img21.gif)
![\begin{gprogram}
all\_change :: Int -> [[Coin]] \\
all\_change 0 = [[]] \\
all...
...
\xx c<-coins, amount>=c, \\
\xx cs<-all\_change (amount - c) ]
\end{gprogram}](img23.gif)
![\begin{gprogram}
all\_change :: Int -> [[Coin]] \\
all\_change 0 = [[]] \\
all...
...
\xx c<-coins, amount>=c, \\
\xx cs<-all\_change (amount - c) ]
\end{gprogram}](img23.gif)
Template:
![]()
Examples:
![\begin{gprogram}
\redtt{> neglist [1,2,3,4,5]} \\
\x 0 \\
\redtt{> neglist [1,-3,-4,3,4,-5]} \\
\x 3
\end{gprogram}](img32.gif)
Template:
![]()
Examples:
![\begin{gprogram}
\redtt{> gensquares 2 5} \\
\x [4, 16] \\
\redtt{> gensquares 3 10} \\
\x [16, 36, 64, 100]
\end{gprogram}](img34.gif)