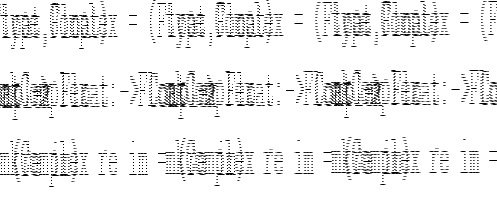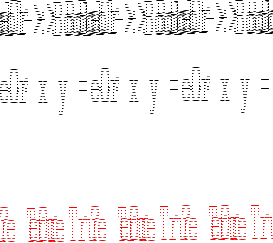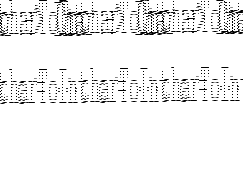CSc 372 - Comparative Programming Languages
4 : Haskell -- Basics

Christian Collberg

Department of Computer Science

University of Arizona

1 The Hugs Interpreter

The Haskell implementation we will be using is called Hugs.
You interact with Hugs by typing commands to the interpreter, much like you would to a powerful calculator:
$\begin{program} \redtt{\$ hugs} \\ \redtt{> 6 * 7} \\ 42 \\ \redtt{> 126 \lq div\lq 3} \\ 4 \end{program}$

2 The Hugs Interpreter...

Haskell programs (known as scripts) are just text files with function definitions that can be loaded into the interpreter using the :load script command:
$\begin{program} \redtt{\$ hugs} \\ \redtt{> :load file.hs} \end{program}$
Haskell scripts take the file extension .hs.

Haskell Types

3 Expressions

When we ``run'' a Haskell program, we actually evaluate an expression, and the result of the program is the value of that expression.
Unlike Java programs. Haskell programs have no statements -- there is no way to assign a new value to a variable for example.

4 Haskell Types

Haskell is strongly typed. This means that every expression has exactly one type.
Haskell is statically typed. This means that the type of an expression can be figured out before we run the program.
The basic types in Haskell include
1. Int (word-sized integers)
2. Integer (arbitrary precision integers)
3. Float (Floating point numbers)
4. Tuples and Lists
5. Strings (really just lists)
6. Function types

5 Type inference

In Java and most other languages the programmer has to declare what type variables, functions, etc have.
We can do this too, in Haskell:
$\begin{program} \redtt{> 6*7 :: Int} \\ 42 \end{program}$
:: Int asserts that the expression 6*7 has the type Int.
Haskell will check for us that we get our types right:
$\begin{program} \redtt{> 6*7 :: Bool} \\ ERROR \end{program}$

6 Type inference...

We can let the Haskell interpreter infer the type of expressions, called type inference.
The command :type expression asks Haskell to print the type of an expression:
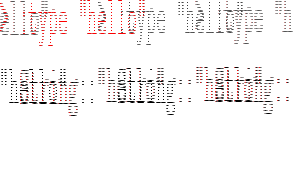
$\begin{program} \redtt{> :type ''hello''} \\ ''hello'' :: String \\ \\ \redtt... ...edtt{> :type True \&\& False :: Bool} \\ True \&\& False :: Bool \end{program}$

Simple Types

7 Int

The Int type is a 32-bit signed integer, similar to Java's int type:
$\begin{program} \redtt{Prelude> (3333333 :: Int) * (44444444444444 :: Int)} \\ Program error: arithmetic overflow \end{program}$
Some Haskell versions may instead overflow the integer (yielding a negative number).

8 Int -- Operators

The normal set of arithmetic operators are available:

Op Precedence Associativity Description

^ 8 right Exponentiation

*, / 7 left Mul, Div

`div` 7 free Division

`rem` 7 free Remainder

`mod` 7 free Modulus

+, - 6 left Add, Subtract

==,/= 4 free (In-) Equality

<,<=,>,>= 4 free Relational Comparison

9 Int...

Note that the div operator has to be in backquotes when used as an infix operator:

$\begin{program} \redtt{> 4*12-6} \\ 42\\ \redtt{> 126 \lq div\lq 3} \\ 42 \\ \redtt{> div 126 3} \\ 42 \end{program}$

10 Int...

The standard precedence and associativity rules apply:

$\begin{xprogram} 1+2-3 \xxxxx $\Rightarrow$ (1+2)-3 \\ 1+2*3 \xxxxx $\Rightarr... ... 2\verb+^+3\verb+^+4 \xxxxx $\Rightarrow$ 2\verb+^+(3\verb+^+4) \end{xprogram}$

$\begin{xprogram} 4==5==6 \xxxxx $\Rightarrow$ \redtxt{ERROR} \\ 12/6/3 \xxxxx ... ...\redtxt{0.666666666666667} \\ 12/(6/3) \xxxxx $\Rightarrow$ 6.0 \end{xprogram}$

11 Integer

Haskell also has an infinte precision integer type, similar to Java's java.math.BigInteger class:

$\begin{program} \redtt{> (3333333 :: Integer) * (44444444444444 :: Integer)} \\ 148148133333331851852 \end{program}$

Integers are the default integer type:

$\begin{program} \redtt{> 2\^{}64} \\ 18446744073709551616 \end{program}$

12 Integer...

Ints and Integers aren't compatible:

$\begin{program} \redtt{> (3333333 :: Integer) * (44 :: Int)} \\ ERROR - Type error in application \end{program}$

but we can convert from an Int to an Integer:

$\begin{program} \redtt{> (toInteger (55 :: Int)) * (66 :: Integer)} \\ 3630 \end{program}$

13 Float and Double

Haskell also has built-in floating point numbers Float and Double:
$\begin{program} \redtt{> sqrt 2 :: Float} \\ 1.414214 \\ \redtt{> sqrt 2 :: Double} \\ 1.4142135623731 \end{program}$
sqrt is a built-in library function.
Double is the default:
$\begin{program} \redtt{> sqrt 2} \\ 1.4142135623731 \end{program}$

14 Char

Literals: 'a', 'b'. Special characters: 'n' (newline).
ASCII: '65' (decimal), 'x41' (hex).
There are standard functions on characters (toUpper, isAlpha, etc) defined in the a separate module Char:
$\begin{program} \redtt{> :load Char} \\ \redtt{> toUpper 'A'} \\ 'A'\\ \redtt{> toUpper 'a'} \\ 'A'\\ \redtt{> ord 'a'} \\ 97 \end{program}$

15 Char -- Built-in Functions

$\begin{gprogram} ord :: Char -> Int \\ char :: Int -> Char \\ toUpper, toLower... ...s$ :: Char -> Bool \\ isUpper,isLower,$\cdots$ :: Char -> Bool \end{gprogram}$

$\begin{gprogram} ord 'a' $\Rightarrow$ 97 \xxxxx toUpper 'a' $\Rightarrow$ 'A'... ...chr 65 $\Rightarrow$ 'A' \xxxxx isDigit 'a' $\Rightarrow$ False \end{gprogram}$

16 String

Strings are really lists of characters.
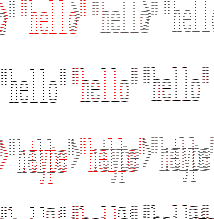
$\begin{program} \redtt{> ''hello''} \\ ''hello''\\ \redtt{> :type ''hello''} \... ...} \\ 5\\ \redtt{> ''hello'' ++ '' world!''} \\ ''hello world!'' \end{program}$
++ does string/list concatenation.

17 Bool

There are two boolean literals, True and False

Op	Precedence	Associativity	Description
`&&`	3	right	logical and
`\|\|`	2	right	logical or
`not`	9	-	logical not

$\begin{gprogram} 3 < 5 \&\& 4 > 2 \xxxxxxxx $\Leftrightarrow$ (3 < 5) \&\& (4 >... ...xxxx $\Leftrightarrow$ True \verb+\vert\vert+ (False \&\& True) \end{gprogram}$

Haskell Functions

18 Functions

Here's the ubiquitous factorial function:
$\begin{gprogram} fact :: Int -> Int \\ fact n = \xxxx if n == 0 then \\ \xxxxx 1 \\ \xxxx else \\ \xxxxx n * fact (n-1) \end{gprogram}$
The first part of a function definition is the type signature, which gives the domain and range of the function:
$\begin{gprogram} \xx fact :: Int -> Int \end{gprogram}$
The second part of the definition is the function declaration, the implementation of the function:
$\begin{gprogram} fact n = if n == 0 then $\cdots$ \end{gprogram}$

19 Functions...

The syntax of a type signature is
$\begin{gprogram} fun\_name :: arg\_types \end{gprogram}$
fact takes one integer input argument and returns one integer result.
The syntax of function declarations:
$\begin{gprogram} fun\_name param\_names = fun\_body \end{gprogram}$
fact is defined recursively, i.e. the function body contains an application of the function itself.
Function application examples:
$\begin{gprogram} fact 1 \xxxx $\Rightarrow$ \x 1 \\ fact 5 \xxxx $\Rightarrow$ \x 120 \\ fact (3+2) \xxxx $\Rightarrow$ \x 120 \end{gprogram}$

List and Tuple Types

20 Lists

A list in Haskell consists of a sequence of elements, all of the same type:

$\begin{program} \redtt{> [1,2,3]} \\ {[1,2,3]}\\ \redtt{> [True,False] :: [Boo... ...\ \redtt{> [1,True]} \\ ERROR \\ \redtt{> length [1,2,3]} \\ 3 \end{program}$

21 Tuples

A Haskell tuple is similar to a record/struct in C - it is a collection of objects of (a limited number of) objects, possibly of different types. Each C struct elements has a unique name, whereas in Haskell you distinguish between elements by their position in the tuple.
Syntax: $(t_1,t_2,\cdots,t_n)$ .

Examples:
$\begin{gprogram} type Complex = (Float,Float) \\ mkComplex :: Float -> Float -> Complex \\ mkComplex re im = (re, im) \end{gprogram}$

22 Tuples...

$\begin{gprogram} type Complex = (Float,Float) \\ mkComplex :: Float -> Float ->... ... addComplex (mkComplex 5 3) (mkComplex 4 2) $\Rightarrow$ (9,5) \end{gprogram}$

Haskell Scripts

23 Editing and Loading Scripts

:load name (or :l name) loads a new Haskell program.
:reload (or :r) reloads the current script.
:edit name (or :e name) edits a script. On Unix you can set the EDITOR environment variable to control which editor to use:
$\begin{program} setenv EDITOR emacs \end{program}$
:? shows all available commands.
:quit quits Hugs.

24 The Offside Rule

When does one function definition end and the next one begin?

$\begin{gprogram} square x = \xxxx x * x \\ \xxxx +2 \\ cube x = $\cdots$ \end{gprogram}$

Textual layout determines when definitions begin and end.

25 The Offside Rule...

The first character after the "=" opens up a box which holds the right hand side of the equation:

OpenBox

Any character to the left of the line closes the box and starts a new definition:

CloseBox

26 Comments

Line comments start with - and go to the end of the line:
$\begin{program} - This is a comment. \end{program}$
Nested comments start with {- and end with -}:
$\begin{program} \{- \\ \x This is a comment. \\ \x \{- \\ \xx And here's another one.... \\ \x -\} \\ -\} \end{program}$

Editing Scripts

27 Emacs

On Unix, emacs is the editor of choice.
Depending on your system, it may be called emacs or xemacs.
For a list of common commands, see the links below.

28 Readings and References

In addition to our textbook, chapters 1-3 of Programming in Haskell, by Graham Hutton, is a good introduction to Haskell: http://www.cs.nott.ac.uk/~gmh/book.html
Emacs Guide: http://www.cs.arizona.edu/classes/cs372/fall03/04.html
Emacs Reference Card: http://www.cs.arizona.edu/classes/cs372/fall03/emacs.html

29 Summary

Haskell has all the basic types one might expect: Ints, Chars, Floats, and Bools.
Haskell functions come in two parts, the signature and the declaration:
$\begin{gprogram} fun\_name :: argument\_types \\ fun\_name param\_names = fun\_body \end{gprogram}$
Many Haskell functions will use recursion.
Haskell doesn't have assignment statements, loop statements, or procedures.
Haskell tuples are similar to records in other languages.

30 Homework

Start Hugs.
Enter the commaint function and try it out.
Enter the addComplex and mkComplex functions and try them out.
Try the standard functions fst x and snd x on complex values. What do fst and snd do?
Try out the Eliza application in /usr/local/hugs98/lib/hugs/demos/Eliza.hs on lectura.

31 Homework...

Write a Haskell function to check if a character is alphanumeric, i.e. a lower case letter, upper case letter, or digit.

$\begin{gprogram} \redtxt{? isAlphaNum 'a'} \\ \x True \\ \redtxt{? isAlphaNum ... ...Num ';'} \\ \x False \\ \redtxt{? isAlphaNum '@'} \\ \x False \end{gprogram}$

32 Homework...

Define a Haskell exclusive-or function.

$\begin{gprogram} eOr :: Bool -> Bool -> Bool \\ eOr x y = $\cdots$ \\ \\ \re... ...lse True} \\ \x True \\ \redtxt{? eOr False False} \\ \x False \end{gprogram}$

33 Homework...

Define a Haskell function charToInt which converts a digit like '8' to its integer value 8. The value of non-digits should be taken to be 0.

$\begin{gprogram} charToInt :: Char -> Int \\ charToInt c = $\cdots$ \\ \\ \r... ...t{? charToInt '0'} \\ \x 0 \\ \redtxt{? charToInt 'y'} \\ \x 0 \end{gprogram}$

Christian S. Collberg
2007-08-23

CSc 372 - Comparative Programming Languages 4 : Haskell -- Basics

CSc 372 - Comparative Programming Languages
4 : Haskell -- Basics