CSc 372 - Comparative Programming Languages
7 : Haskell -- Patterns

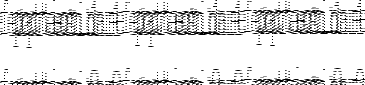
Christian Collberg

Department of Computer Science

University of Arizona

1 Pattern Matching

Haskell has a notation (called patterns) for defining functions that is more convenient than conditional (if-then-else) expressions.
Patterns are particularly useful when the function has more than two cases.

Pattern Syntax:
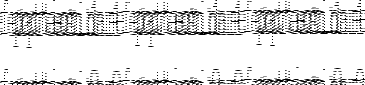
$\begin{gprogram} function\_name pattern\_1 = expression\_1 \\ function\_name pa... ...2 \\ \xx $\cdots$\ \\ function\_name pattern\_n = expression\_n \end{gprogram}$

2 Pattern Matching...

$\begin{gprogram} fact n = if n == 0 then \\ \xx 1 \\ \x else \\ \xx n * fact (n-1) \end{gprogram}$

fact Revisited:
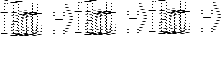
$\begin{gprogram} fact :: Int -> Int \\ fact 0 = 1 \\ fact n = n * fact (n-1) \end{gprogram}$

3 Pattern Matching...

Pattern matching allows us to have alternative definitions for a function, depending on the format of the actual parameter. Example:

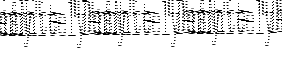
$\begin{gprogram} isNice ''Jenny'' = ''Definitely'' \\ isNice ''Johanna'' = ''Maybe'' \\ isNice ''Chris'' = ''No Way'' \end{gprogram}$

4 Pattern Matching...

We can use pattern matching as a design aid to help us make sure that we're considering all possible inputs.
Pattern matching simplifies taking structured function arguments apart. Example:

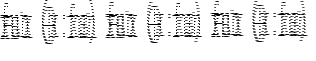
$\begin{gprogram} fun (x:xs) = x $\oplus$\ fun xs \\ \xx $\Leftrightarrow$\ \\ fun xs = head xs $\oplus$\ fun (tail xs) \end{gprogram}$

5 Pattern Matching...

When a function is applied to an argument, Haskell looks at each definition of until the argument matches one of the patterns.

$\begin{gprogram} not True = False \\ not False = True \end{gprogram}$

6 Pattern Matching...

In most cases a function definition will consist of a number of mutually exclusive patterns, followed by a default (or catch-all) pattern:

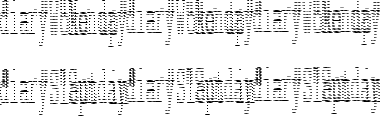
$\begin{gprogram} diary ''Monday'' = ''Woke up'' \\ diary ''Sunday'' = ''Slept i... ... in'' \\ diary ''Tuesday'' $\Rightarrow$\ ''Did something else'' \end{gprogram}$

7 Pattern Matching - Integer Patterns

There are several kinds of integer patterns that can be used in a function definition.

Pattern Syntax Example Description

variable var_name fact n = $\cdots$ n matches any argument

constant literal fact 0 = $\cdots$ matches the value

wildcard _ five _ = 5 _ matches any argument

(n+k) pat. (n+k) fact (n+1) = $\cdots$ (n+k) matches any integer $\geq k$

8 Pattern Matching - List Patterns

There are also special patterns for matching and (taking apart) lists.

Pattern	Syntax	Example	Description
cons	(x:xs)	len (x:xs) = $\cdots$	matches non-empty list
empty	[ ]	len [ ] = 0	matches the empty list
one-elem	[x]	len [x] = 1	matches a list with exactly 1 element.
two-elem	[x,y]	len [x,y] = 2	matches a list with exactly 2 elements.

9 The `sumlist` Function

Using conditional expr:
$\begin{gprogram} sumlist :: [Int] -> Int \\ sumlist xs = \= if xs == [\ ] then 0 \\ \x else head xs + sumlist(tail xs) \end{gprogram}$

Using patterns:
$\begin{gprogram} sumlist :: [Int] -> Int \\ sumlist [\ ] = 0 \\ sumlist (x:xs) = x + sumlist xs \end{gprogram}$

Note that patterns are checked top-down! The ordering of patterns is therefore important.

10 The `length` Function Revisited

Using conditional expr:
$\begin{gprogram} len :: [Int] -> Int \\ len s = \xxx if s == [\ ] then 0 else 1 + len (tail s) \end{gprogram}$

Using patterns:
$\begin{gprogram} len :: [Int] -> Int \\ len [\ ] = 0 \\ len (\_:xs) = 1 + len xs \end{gprogram}$

Note how similar len and sumlist are. Many recursive functions on lists will have this structure.

11 The `fact` Function Revisited

Using conditional expr:
$\begin{gprogram} fact n = if n == 0 then 1 else n * fact (n-1) \end{gprogram}$

Using patterns:
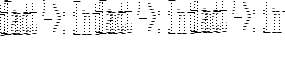
$\begin{gprogram} fact' :: Int -> Int \\ fact' 0 = 1 \\ fact' (n+1) = (n+1) * fact' n \end{gprogram}$

Are fact and fact' identical?
$\begin{gprogram} fact (-1) \xxxx $\Rightarrow$\ \redtxt{Stack overflow} \\ fact' (-1) \xxxx $\Rightarrow$\ \redtxt{Program Error} \end{gprogram}$
The second pattern in fact' only matches positive integers ( $\geq 1$ ).

12 Summary

Functional languages use recursion rather than iteration to express repetition.
We have seen two ways of defining a recursive function: using conditional expressions (if-then-else) or pattern matching.
A pattern can be used to take lists apart without having to explicitly invoke head and tail.
Patterns are checked from top to bottom. They should therefore be ordered from specific (at the top) to general (at the bottom).

13 Homework

Define a recursive function addints that returns the sum of the integers from 1 up to a given upper limit.
Simulate the execution of addints 4.

$\begin{gprogram} addints :: Int -> Int \\ addints a = $\cdots$\ \\ \\ \redtxt{? addints 5} \\ \x 15 \\ \\ \redtxt{? addints 2} \\ \x 3 \end{gprogram}$

14 Homework

Define a recursive function member that takes two arguments - an integer x and a list of integers L - and returns True if x is an element in L.
Simulate the execution of member 3 [1,4,3,2].

$\begin{gprogram} member :: Int -> [Int] -> Bool \\ member x L = $\cdots$\ \\ \... ...[1,2,3]} \\ \x True \\ \redtxt{? member 4 [1,2,3]} \\ \x False \end{gprogram}$

15 Homework

Write a recursive function memberNum x L which returns the number of times x occurs in L.
Use memberNum to write a function unique L which returns a list of elements from L that occurs exactly once.

$\begin{gprogram} memberNum :: Int -> [Int] -> Int \\ unique :: [Int] -> Int \\ ... ...[1,5,2,3,5,5]} \\ \x 3\\ \redtxt{? unique [2,4,2,1,4]} \\ \x 1 \end{gprogram}$

16 Homework

Ackerman's function is defined for nonnegative integers:

$\begin{displaymath}\begin{array}{lll} A(0,n) & = & n + 1 \\ A(m,0) & = & A(m - 1, 1) \\ A(m,n) & = & A(m - 1, A(m,n - 1)) \end{array} \end{displaymath}$

Use pattern matching to implement Ackerman's function.
Flag all illegal inputs using the built-in function error S which terminates the program and prints the string S.

$\begin{gprogram} ackerman :: Int -> Int -> Int \\ ackerman 0 5 $\Rightarrow$\ 6 \\ ackerman (-1) 5 $\Rightarrow$\ \redtxt{ERROR} \end{gprogram}$

Christian S. Collberg
2007-09-03

CSc 372 - Comparative Programming Languages 7 : Haskell -- Patterns

CSc 372 - Comparative Programming Languages
7 : Haskell -- Patterns