CSc 520
Principles of Programming Languages
:

Christian Collberg

Department of Computer Science

University of Arizona

1 Denotational Semantics

• Denotational semantics gives the meaning of a program in terms of mathematical objects: integers, booleans, tuples, and functions.
• The basic idea is to associate a mathematical object with each phrase of the language:
  • The phrase denotes the mathematical object.
  • The object is the denotation of the phrase.
• Definitions in Denotational Semantics are compositional:
  • The denotation of a language construct is defined in the denotations of its sub-phrases.

2 Meaning Brackets

• We use the emphatic (or Strachey or meaning) brackets to enclose pieces of abstract syntax, as in
  
  $$\Sem{p}.$$
  
  

• If $p$ is a phrase in the language, we define a mapping $\mathit{meaning}$ such that
  
  $$\mathit{meaning}\Sem{p}$$
  
  
  is a mathematical entity that models the semantics of $p$.

3 Meaning Brackets -- Examples

• Addition in an imperative language:
  $$\begin{eqnarray*} \mathit{evaluate}\Sem{E_1+E_2}\mathrm{sto}& = & \mathtt{comput... ...mathrm{sto}\\ n & = & \mathit{evaluate}\Sem{E_2}\ \mathrm{sto} \end{eqnarray*}$$
  
  

• The expressions $2*4$, $(5+3)$, $008$, $8$ all denote the same abstract object, 8:
  $$\begin{eqnarray*} \mathit{meaning}\Sem{2*4} & = & \mathit{meaning}\Sem{(5+3)} = \\ \mathit{meaning}\Sem{008} & = & \mathit{meaning}\Sem{8} = 8 \end{eqnarray*}$$
  
  

4 Denotational Specification

• A denotational specification consists of five parts:
  1. Syntactic categores
  2. Abstract production rules
  3. Semantic domains
  4. Semantic functions
  5. Semantic equations.

Example -- A Language of Numerals

5 Denotational Specification

Syntactic Domains:

• $N$ : Numeral
• $D$ : Digit

Abstract Production Rules:

Semantic Domains:

• Number = $\{0,1,2,3,4,\ldots\}$

6 Denotational Specification...

Semantic Functions:

$$\begin{eqnarray*} \mathit{value}& : & \mathrm{Numeral} \rightarrow \mathrm{Numb... ...thit{digit}& : & \mathrm{Digit} \rightarrow \mathrm{Number} \\ \end{eqnarray*}$$

Semantic Equations:

$$\begin{eqnarray*} \mathit{value}\Sem{N\ D} & = & 10 * \mathit{value}\Sem{N} + \... ...= & 0 \\ & \vdots & \\ \mathit{digit}\Sem{\:9:} & = & 9 \\ \end{eqnarray*}$$

7 Example

• Let's see how the meaning of the phrase 6:5: would be derived:
  $$\begin{eqnarray*} \mathit{value}\Sem{\:6:\:5:} & = & 10*\mathit{value}\Sem{\:6:... ...git}\Sem{\:6:} + 5 \\ & = & 10*6 + 5 \\ & = & 60 + 5 = 65\\ \end{eqnarray*}$$
  
  

8 Example...

• And the meaning of the phrase 0:8:8::
  $$\begin{eqnarray*} \mathit{value}\Sem{\:0:\:8:\:8:} & = & 10*\mathit{value}\Sem{... ...git}\Sem{\:0:} + 0) + 8\\ & = & 10*(10*0 + 0) + 8\\ & = & 8 \end{eqnarray*}$$
  
  

• Note that
  
  $$\mathit{value}\Sem{\:0:\:8:\:8:} = \mathit{digit}\Sem{\:8:} = \mathit{value}\Sem{\:8:} = 8$$
  
  

The Semantics of Wren

9 Imperative Languages

• Wren is an imperative language.
• Programs consist of commands (statements).
• Commands alter a store, a global data structure simulating computer memory.
• The program updates the store until the required result is reached.
• The most important command is the assignment statement which modifies the store.
• Basic program control consists of sequencing, selection, and iteration (;, if, while).

10 Abstract Syntactic Domains

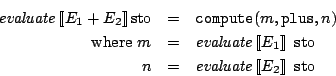
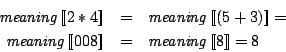
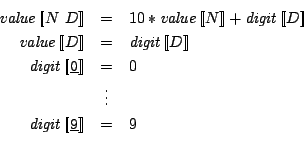
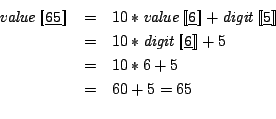
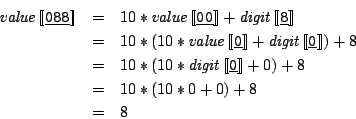
These are the abstract syntactic domains of Wren:

$P$:

$\mathrm{Program}$

$C$:

$\mathrm{Command}$

$D$:

$\mathrm{Declaration}$

$T$:

$\mathrm{Type}$

$E$:

$\mathrm{Expression}$

$O$:

$\mathrm{Operator}$

$N$:

$\mathrm{Numeral}$

$I$:

$\mathrm{Identifier}$

11 Abstract Syntax of Wrens

12 Semantic Domains of Wren

• $\mathbf{SV}$ (storable values) represents the values that may be placed in the store.
• $\mathbf{EV}$ (expressible or first-class values) represents the values that expressions can produce.

$$\begin{eqnarray*} \mathrm{Integer}& = & \{\ldots -2, -1, 0, 1, 2, \ldots \} \\ ... ...\mathrm{Identifier}\rightarrow (\mathbf{SV}+ \mathit{undefined}) \end{eqnarray*}$$

13 Semantic Functions of Wren

• The value of an expression depends on the values of variables in the store:
  $$\begin{eqnarray*} \mathit{evaluate} & : & \mathrm{Expression}\rightarrow (\mathrm{Store}\rightarrow \mathbf{EV}) \end{eqnarray*}$$
  
  

• Commands (statements) can modify the store:
  $$\begin{eqnarray*} \mathit{execute} & : & \mathrm{Command}\rightarrow (\mathrm{Store}\rightarrow \mathrm{Store}) \end{eqnarray*}$$
  
  

• The meaning of a program is its resulting store:
  $$\begin{eqnarray*} \mathit{meaning} & : & \mathrm{Program}\rightarrow \mathrm{Store} \end{eqnarray*}$$
  
  

• The meaning of a number is handled elsewhere:
  $$\begin{eqnarray*} \mathit{value} & : & \mathrm{Numeral}\rightarrow \mathbf{EV} \end{eqnarray*}$$
  
  

14 Commands

• The semantics of sequenced commands:
  $$\begin{eqnarray*} \mathit{execute}\Sem{C_1; C2} & = & \mathit{execute}\Sem{C_2} \circ\ \mathit{execute}\Sem{C1} \end{eqnarray*}$$
  
  
  This could also be written as
  $$\begin{eqnarray*} \mathit{execute}\Sem{C_1; C2} & = & \mathit{execute}\Sem{C_2} (\mathit{execute}\Sem{C1}\mathrm{sto}) \end{eqnarray*}$$
  
  

• $\mathbf{skip}$ does not affect the store:
  $$\begin{eqnarray*} \mathit{execute}\Sem{\mathbf{skip}}\mathrm{sto}& = & \mathrm{sto} \end{eqnarray*}$$
  
  

• The assignment statement evaluates the right-hand-side and produces an updated store:
  $$\begin{eqnarray*} \mathit{execute}\Sem{I\mathbf{:=}\ E}\mathrm{sto}& = & \mathi... ...to}(\mathrm{sto},I,(\mathit{evaluate}\Sem{E}\ \mathrm{sto})) \\ \end{eqnarray*}$$
  
  

15 Commands...

• Conditionals:
  $$\begin{eqnarray*} \mathit{execute}\Sem{\mathbf{if}\ E\ \mathbf{then}\ C}\mathrm... ...mathrm{where}\ p & = & \mathit{evaluate}\Sem{E}\ \mathrm{sto}\\ \end{eqnarray*}$$
  
  

16 Commands...

• Loops:
  $$\begin{eqnarray*} \mathit{execute}\Sem{\mathbf{while}\ E\ \mathbf{do}\ C}\mathrm... ...mathrm{where}\ p & = & \mathit{evaluate}\Sem{E}\ \mathrm{sto}\\ \end{eqnarray*}$$
  
  

• Here we have factored out the looping behavior into a special recursive function loop.

17 Expressions

$$\begin{eqnarray*} \mathit{evaluate}\Sem{I}\mathrm{sto}& = & \mathbf{if}\ v=\math... ...mathrm{sto}\\ n & = & \mathit{evaluate}\Sem{E_2}\ \mathrm{sto} \end{eqnarray*}$$

18 Expressions...

$$\begin{eqnarray*} \mathit{evaluate}\Sem{E_1/E_2}\mathrm{sto}& = & \mathbf{if}\ n... ...mathrm{sto}\\ q & = & \mathit{evaluate}\Sem{E_2}\ \mathrm{sto} \end{eqnarray*}$$

A Haskell Prototype

19 Abstract Syntax

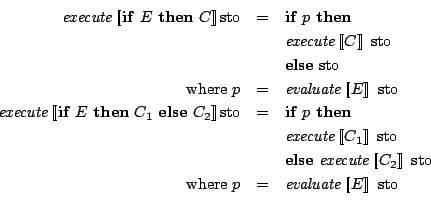
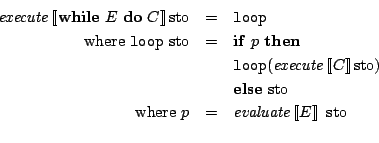
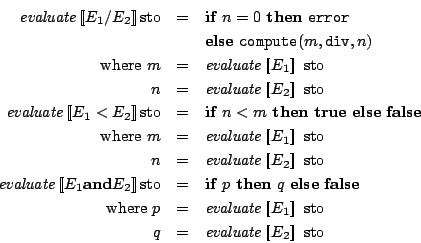
type Num =  Rational 

data SV    = IVal Num | BVal Bool | Undefined

type Identifier = String

data Operator  = Add | Sub | Mul | Minus | Div | Not | 
                 Or | And | Lt | Gt | Eq | Ne | Le | Ge

data Expression = Id String |
                  LitInt Num |
                  TrueVal |
                  FalseVal |
                  Unary Operator Expression |
                  Binary Expression Operator Expression

20 Abstract Syntax...

data Program = Prog [Declaration] Command

data Declaration = Var [Identifier] Type 

data Type = IntType | BoolType

data Command = Skip |
               Assign String Expression |
               Read String |
               Write Expression |
               IfThen Expression Command |
               IfThenElse Expression Command Command |
               While Expression Command |
               Seq Command Command

21 Expressions

bcompute :: SV -> Operator -> SV -> SV
bcompute (IVal a) Add (IVal b) = (IVal (a + b))
bcompute (IVal a) Mul (IVal b) = (IVal (a * b))
bcompute (IVal a) Div (IVal b) = 
      if b==0 then error "Division by 0" 
      else         (IVal (toRational(a / b)))
bcompute (IVal a) Sub (IVal b) = (IVal (a - b))
bcompute (BVal a) And (BVal b) = (BVal (a && b))
bcompute (BVal a) Or  (BVal b) = (BVal (a || b))
bcompute (IVal a) Lt  (IVal b) = (BVal (a < b))
bcompute (IVal a) Gt  (IVal b) = (BVal (a > b))
bcompute (IVal a) Le  (IVal b) = (BVal (a <= b))
bcompute (IVal a) Ge  (IVal b) = (BVal (a >= b))
bcompute (IVal a) Eq  (IVal b) = (BVal (a == b))
bcompute (IVal a) Ne  (IVal b) = (BVal (not (a == b)))

22 Expressions...

ucompute :: Operator -> SV -> SV
ucompute Minus (IVal b) = (IVal (- b))
ucompute Not (BVal b) = (BVal (not b))

23 Expressions...

evaluate :: Expression -> Store -> SV
evaluate (Id id) sto = 
      if val == Undefined then val else val 
         where val = applySto sto id
evaluate (LitInt n) sto = (IVal n)
evaluate (TrueVal) sto = (BVal True)
evaluate (FalseVal) sto = (BVal False)
evaluate (Unary op r) sto = ucompute op n
   where n = evaluate r sto
evaluate (Binary l op r) sto = bcompute m op n
   where m = evaluate l sto
         n = evaluate r sto

24 Expressions -- Examples

> s1
[("b",True),("a",5 % 1)]

> evaluate (Binary (LitInt 5) Add (LitInt 6)) s1
11 % 1

> evaluate (Binary (LitInt 5) Add (Id "a")) s1
10 % 1

> evaluate (Binary (Binary (LitInt 6) Mul (LitInt 2)) Add (Id "a")) s1
17 % 1

25 Commands

execute :: Command -> Store -> Store
execute (Skip) sto = sto
execute (Assign id e) sto = updateSto sto id (evaluate e sto)
execute (Seq c1 c2) sto = execute c2 (execute c1 sto)
execute (IfThen b c) sto = 
     if (evaluate b sto) == (BVal True) then 
         execute c sto 
     else sto
execute (IfThenElse b c1 c2) sto = 
     if (evaluate b sto) == (BVal True) then 
         execute c1 sto 
      else execute c2 sto
execute (While b c) sto = loop sto
   where loop sto = if (evaluate b sto) == (BVal True) then 
                    (loop (execute c sto)) else sto

26 Commands -- Examples

> s1
[("b",True),("a",5 % 1)]

> execute (Assign "a" (LitInt 9)) s1
[("a",9 % 1),("b",True)]

> execute (IfThen (Unary Not (Id "b")) (Assign "a" (LitInt 9))) s1
[("b",True),("a",5 % 1)]

> execute (While (Binary (Id "a") Lt (LitInt 10)) (Assign "a" (Binary (Id "a") Add (LitInt 1)))) s1
[("a",10 % 1),("b",True)]

27 Store

type Store = [(Identifier,SV)]

emptySto:: Store
emptySto = []

updateSto::  Store -> Identifier -> SV -> Store
updateSto env id val = 
   (id,val) : (filter (\ (x,_) -> not(id==x)) env)

applySto::  Store -> Identifier -> SV
applySto env id = 
   snd (foldl (\ r c -> if id==(fst r) then r else c) ("",Undefined) env)

28 Store -- Examples

s1 = updateSto (updateSto emptySto "a" (IVal 5)) "b" (BVal True) 

> s1
[("b",True),("a",5 % 1)]

> applySto s1 "a"
5 % 1

> applySto s1 "b"
True

> applySto emptySto "a"
Undefined

29 Readings and References

• Read pp. 271-277, 285-310, in Chapter 9 of Syntax and Semantics of Programming Languages, by Ken Slonneger and Barry Kurtz, http://www.cs.uiowa.edu/~slonnegr/plf/Book.

30 Acknowledgments

• Much of the material in this lecture on Denotational Semantics is taken from the book Syntax and Semantics of Programming Languages, by Ken Slonneger and Barry Kurtz, http://www.cs.uiowa.edu/~slonnegr/plf/Book.