So far, we have not discussed the issue of how the appropriate path is found for a given message. In many cases, this is trivial. For example, a path is often used like a file descriptor, a window handle, or a socket descriptor. In these cases, paths are created specifically for communicating a certain kind of data and the appropriate path is known from the context in which it is being used. In other cases, however, there is no such context and the appropriate path is implicitly determined by the data itself. The most notable area where this is the case is for the networking subsystem. Networking protocols typically require hierarchical demultiplexing for arriving network packets. For example, when a network packet arrives at an Ethernet adapter [65], the Ethernet type field needs to be looked up to determine whether the packet happens to be, e.g., an IP packet or an ARP packet. If it is an IP packet, it is necessary to look up the protocol field to determine whether it is a UDP or TCP packet, and so on. This hierarchical demultiplexing is suboptimal since as more knowledge becomes available with each demultiplexing step, another path might become more suitable to process that packet.
To alleviate the hierarchical demultiplexing problem, Scout uses a packet classifier that factors all demultiplexing operations to the earliest possible point. This lets Scout pick a path and start processing a packet only after as many demultiplexing decisions as possible have been made. Of course, a solution that would be better still (as far as Scout is concerned) would be to modify the header of the lowest layer protocol to include a field that can store the path id [56]. That way, demultiplexing could be reduced to a simple table lookup. However, since Scout needs to be able to interoperate with existing networking infrastructure, this is not always an option.
The factoring of demultiplexing decisions is best explained with an example. Suppose a UDP packet were received by an Ethernet adapter. The processing that would occur with hierarchical demultiplexing is shown on the left, with a classifier on the right:
| Without Classifier: | With Classifier:49> |
| Ethernet processing | Ethernet demux => it's an IP packet |
| Ethernet demux => it's an IP packet | IP demux => it's a UDP packet |
| IP processing | Ethernet processing |
| IP demux => it's a UDP packet | IP processing |
| UDP processing | UDP processing |
|
|
|
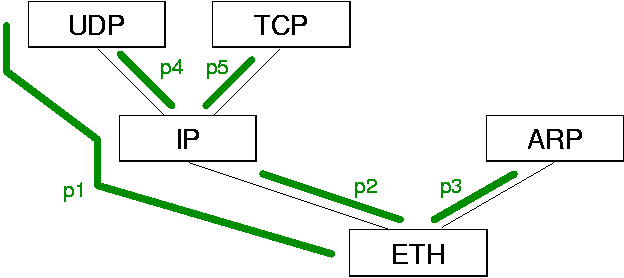
The way packet classifiers are used in Scout is unique and therefore worth discussing in some more detail. In particular, their role with respect to dynamic routing decisions is interesting. Consider Figure 15. It would be preferable to process every incoming packet destined for UDP using path p1. Unfortunately, this ideal case cannot always be achieved. For example, the UDP packets may have been fragmented by IP, or IP might have employed a non-trivial data transformation, such as encryption or compression. In all three cases, some protocol headers may not be available to the classifier. Scout copes with this problem by employing short paths as necessary. In the example, an IP fragment would have to be processed first by path p2 and then by path p4, even though this would be less optimal than processing with p1.

The specifics of how the partial classification problem is solved in
Scout are explained next. As previously suggested, the Ethernet
module (ETH) employs a classifier to decide whether a packet
should be processed using path p1, p2, or p3. Suppose an IP fragment
that does not contain the higher-level headers arrives at the Ethernet
adapter. Without higher-level headers, the best the classifier may be
able to do is to determine that path p2 is appropriate for processing
the fragment.
This example shows that, in Scout, a classifier is not something specific to network drivers, but instead is a mechanism that can be employed by any module that needs to make a dynamic routing decision based on the contents of the data being communicated. Typically, each network device driver uses a classifier which is invoked when a packet receive interrupt is processed, but other modules may use their own classifiers if necessary.
Since Scout is a modular system, we would like to be able to express classification in a modular fashion as well. That way, the complete classifier can be built automatically from partial classification algorithms that are specified by the module that appear along a path. Note that a modular specification of the classifier does not necessarily imply a modular implementation, though this is true for the current Scout implementation.
As discussed earlier, classifiers are used in Scout by any module that may need to make a dynamic routing decision based on the contents of a message. The task of a classifier can therefore be described as: given a module m and a message, determine a path that is appropriate for processing the given message. Since it is module m that is making the routing decision, the path must start at that module.
The classification task can be implemented in an iterative fashion using partial classifiers of the following form: given a set of paths and a message, determine the subset of paths that qualify for the processing of the given message, the module that needs to make the next (refining) classification (if any), and the message for that next module. The message for the next module is normally the same as the original message, except that the protocol header at the front of the message will have been stripped off. This scheme works as long as the classification problem is locally hierarchical. The ramifications of this constraint will be explained in detail in Section 3.4.3.1. For now, we assume that the Scout classification problem satisfies this constraint. Using such partial classifiers, the problem can be solved with the pseudo-code shown in Figure 16.
1 classify (Module m, Message d):
2 pset <- Ø
3 for (p in pset)
4 if (p.end[0].module == m || p.end[1].module == m)
5 pset <- pset \cup {p};
6 path <- NULL
7 while (m != NULL ^ pset != Ø) do
8 <m, pset, d> <- m.demux (pset, d)
9 for (p in pset)
10 if (p.end[0].module == m || p.end[1].module == m)
11 path <- p
12 return path
Lines 2--5 of the pseudo-code determine the set of paths that either
begin or end at module m. This path set is stored in variable
pset. Then, as long as there is a module m and a set of
candidate paths pset, the partial classifier demux of
module m is invoked (line 8), passing the current candidate set
and message d as parameters. The partial classifier is
expected to return the next module m that should refine the
classification, a new candidate set pset, and a new message
d. If there is no next module, then m will be
NULL. Given the new candidate set, the code checks in lines
9--11 whether there is any path p in pset that ends at
module m. If there is such a path, it is suitable for
processing the original message and is stored in variable path.
Scout does not allow ambiguity in classification, meaning that there
is at most one path per iteration that is suitable for processing the
message.
We observe that the classification process can be viewed as a tree traversal where the partial classifiers are used to select the next node to be visited and where each node corresponds to a path set. This tree-traversal can be implemented efficiently. Note that the search tree contains one node per module and per path set. In Scout, demultiplexing nodes have the following structure:
typedef struct {
long numPaths;
Path path;
Module nextModule;
} * DemuxNode;
Given the definition of a demux node, the partial classifiers are functions with a prototype shown below (Msg is the Scout type to represent a message, i.e., a sequence of data bytes):
Note that the return value is a path. This is because each partial classifier will invoke the partial classifier of the next module, if necessary. Thus, the tree traversal loop is implicitly implemented as a sequence of nested calls. Also note that the partial classifier function of each module is stored in the module object (see Section 3.2.3.2). When a new module object is created, the module must initialize member demux in the object to the module's partial classifier function.Path (*DemuxFunc) (DemuxNode pset, Msg m);
The next question is how the tree of demux nodes is created and maintained. Suppose a new path p has been created. The first stage s in this path is p->end[0]. If we assume that the module at which the path starts uses a hash table h to implement the partial classifier function and that the module's partial key for path p is k, then the first module in the path can update its demux node by calling function updateDemuxNode passing s, h, k and NULL as arguments in this order. The updateDemuxNode function is illustrated with the pseudo-code shown in Figure 17.
1 void
2 updateDemuxNode (Stage s, HashTable h, Key k, DemuxNode pn) {
3 dk = concat (pn, k);
4 n = hashLookup (h, dk);
5 if (!n) {
6 n = new (DemuxNode);
7 n->numPaths = 0;
8 n->path = NULL;
9 n->nextModule = next module in path;
10 hashEnter (h, dk, n);
11 }
12 if (s == s->path->end[1])
13 n->path = s->path;
14 else if (pn)
15 n->path = pn->path;
16 ++n->numPaths;
17 }
In line 3, the function concatenates the bits of the previous demux node with those for the partial key k. Since this is the first stage in the path, there is no previous demux node (pn is NULL), so dk equals k. In line 4, the demux node is looked up using the demux key. If no demux node exists for that key yet, lines 6--10 create a new node and enter it in the hash table. In lines 12--15, the path member of the node is updated if necessary. Specifically, if stage s is the last stage of the path, then path p can be used for any message that gets classified at least to node n. If the end of the path has not been reached yet, n->path is simply set to the path of the previous node, or left unmodified if there is no previous node. In line 16, the number of paths in the path set represented by n is incremented.
A demux node is normally updated during the establish callback of a stage. Note that the same routine can be used to update the demux nodes for all stages in a newly created path. The only difference compared to the first stage is that pn, the previous node pointer is no longer NULL. This pointer is passed as attribute PREVIOUS_DEMUX_NODE in the attribute set passed to each stage. Note that, in general, classification can be initiated at either end of the path. Thus, when descending in the establish callback chain, this attribute points to the previous demux node with respect to classification in the forward direction, but once the end of the path is reached, the attribute changes its meaning into representing the previous node with respect to classification in the backward direction.
Note that the updateDemuxNode function works properly even in the case of a module that does not perform demultiplexing in the given direction. In such a case, the key k simply has zero length. While the function works properly, this special case can be optimized by simply updating the nextModule pointer of the previous node to the next module along the path. This has the effect that modules that do not perform classification in the given direction are skipped.
With this setup, a partial classification function is typically implemented similar to that shown in Figure 18. First, line 2 extracts the partial demux key from the message (typically from a header) and stores it in k. Then the bits of the previous demux node and the partial key are concatenated and looked up in the hash table. If an appropriate demux node exists for the message, the classification is refined by calling the partial classifier function of the next module. If that classification succeeds, the path found is returned. Otherwise, the path associated with demux node n is returned (which may be NULL if no suitable path exists).
1 Path demux (DemuxNode pn, Msg m) {
2 extract key k from m;
3 dk = concat (pn, k);
4 n = hashLookup (h, dk);
5 if (n) {
6 if (n->nextModule)
7 path = n->nextModule->demux (n, msg);
8 if (path)
9 return path;
10 return n->path;
11 }
12 return NULL;
13 }
As alluded to before, the classification scheme as described so far works for locally hierarchical classification problems. By this we mean that each partial classifier can make its decision in isolation. Unfortunately, for real networking protocols, the problem is not limited to this special case. It is hierarchical, but only at the global level.
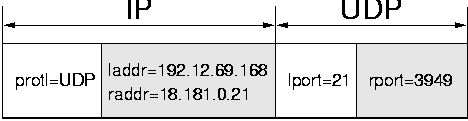
This is illustrated in Figure 19, which shows the IP and UDP header fields that are used for classification purposes. IP uses the protocol field, and the local and remote addresses. In the figure, these fields are labelled protl, laddr, and raddr respectively. For UDP, the fields used are the local and remote port number; lport and rport in the figure. For paths that represent actively opened network connections (active paths), all five fields need to be matched. On the other hand, for paths representing passively opened connections (passive paths), only the protocol field and local port field need to be matched. This means that the classification process is still hierarchical, but only at the global level.
| protl | laddr | raddr | lport | rport | maps to: | |
| <UDP, | any | any | 21, | any> | => | path 1 (passive) |
| <UDP, | 192.12.69.168, | 18.181.0.21, | 21, | 3949> | => | path 2 (active) |
Suppose a system has the mappings shown in Table 3 in place. If a packet with the fields <protl=UDP, laddr=192.12.69.168, raddr=18.181.0.21, lport=21, rport=3950> were to arrive, then IP could not make a proper decision as to whether the path subset it passes to UDP should include both the active path and the passive path or only the former. If it were to pass on the active path only, classification would erroneously fail, since there is no active path matching the packet. On the other hand, if it were to pass on both paths, then classification would be erroneously ambiguous for packets that belong to the active path. That is, whether IP should use the fields for an active path or the a passive path depends on the classification decision of UDP. Since IP cannot know how UDP's partial classifier works, it may make the wrong choice no matter how careful it is.
To solve this problem in general, it is necessary to try to find a path with the most specific keys first and, if that fails, backtrack and try the same with a less specific key. For example, networking protocols such as IP that distinguish between active and passive keys, could use logic similar to the one shown in Figure 20.
1 path <- try_active_demux (pn, m); 2 if (!path) 3 path <- try_passive_demux (pn, m);
In the figure, functions try_active_demux and try_passive_demux correspond to classifiers as shown in Figure 18 that use the active and passive keys, respectively. With this kind of backtracking in place, it is guaranteed that the correct combination of keys is eventually found and therefore classification is guaranteed to find the correct path, if it exists.
Unfortunately, adding backtracking causes classification complexity to
increase from O(N) to O(2N), where N is the number of partial
demux functions that require backtracking. Even though this involves
exponential complexity, it might be quite practical since the number
of demultiplexing layers is rarely bigger than four or five (not all
of which may require backtracking). Better still, for networking
protocols backtracking can be limited in a way that allows bringing
back classification to linear time complexity. Observe that for the
vast majority of systems, it is acceptable to limit paths to use
either all active or all passive keys.
Most demultiplexing occurs in modules implementing networking protocols, but it certainly is desirable to be able to connect modules implementing networking protocols and other modules without any bad consequences (as long as the module graph is sensible). For example, a filter that converts MPEG-encoded video into a sequence of images should work properly independent of whether its input is fed from a disk or the network. Similarly, it should be possible to insert a filter (e.g., one that counts the number of bytes that pass through it) between a pair of networking protocols (e.g., TCP and IP) and have the system operate as expected.
This kind of support requires answering how demultiplexing needs to be interpreted with respect to modules that do not perform any demultiplexing themselves. Fortunately, this is straight-forward in Scout: a module simply needs to ensure that its partial classifier applies the same data transformations as the actual processing. If the data is not transformed at all (such as in the byte-counting filter mentioned previously), then the partial classifier would not have to do anything either. On the other hand, if a module modifies all data passing through it---e.g., by complementing it---then the partial classifier would have to do the same. Of course, if the operation is complex or computationally expensive (such as encryption), then the module might prefer not to let classification proceed beyond itself. A module can do this by blocking the PREVIOUS_DEMUX_NODE attribute during the establish callback. When a module does this, it implies that the earlier modules have to be able to make an accurate enough classification so that a unique path can be found even without the help of the partial classifiers in later modules.
To gain a better understanding of the Scout classifier, we compare it to other existing packet classifiers. The two classifiers with the best published performance are DPF [30] and PathFinder [5]. Unfortunately, the existing implementation of PathFinder is not 64-bit clean and even on 32-bit systems there appear to be problems that prevent it from working reliably. For this reason, the remainder of this discussion is limited to a comparison with DPF. The available DPF implementation is version 2.0 beta, which is a re-implementation of the version presented in [30]. The measurements for this comparison were performed in a user-level test environment running on Linux on an AlphaStation 600/333. This machine uses a 21164 Alpha chip running at 333MHz. All measurements were done with warm caches. Measurements not reported here indicated that the slowdown due to cold caches is significant, but comparable for the two versions and therefore of no particular interest to this discussion. To make the comparison with DPF more meaningful, the Scout classifier was implemented assuming messages are represented as a linear sequence of bytes (the Scout kernel uses a more general tree of linear byte sequences instead).
| Scout | DPF v2.0 | |
| Expressiveness | universal | limited |
| Trust assumed | yes | no |
| Static size of code and data [byte] | 4,901 | 122,311 |
| Lookup active path [µs] | 0.75 | 0.56 |
| Lookup passive path [µs] | 1.45 | 0.65 |
| Insert passive path [µs] | 3.70 | 24.2 |
| Remove passive path [µs] | 1.02 | 3.78 |
| Bytes per filter | 56 | 8,440 |
Table 4 presents a summary of the two classifiers. The row labelled Expressiveness shows that the Scout classifier is universal. This is because the partial demux functions are written in ordinary C and because an exhaustive tree search can be performed if necessary. In contrast, DPF version 2 filters can make use of only two kinds of operators. The first kind supports testing a bitfield in the message contents for equality with either a constant or another bitfield in the message. The second kind of operators support dropping bytes from the front of the message. Both dropping by a constant or a variable number of bytes is supported. A filter can achieve the latter by specifying a bitfield in the message contents that determines the possibly scaled number of bytes to drop. Unfortunately, this feature did not work properly for the Alpha architecture in the beta version of DPF v2.0 that was available at the time of this writing. For this reason, the TCP/IP filters used in the measurements assumed fixed size headers (which is not realistic, as both TCP and IP support header options).
The row labelled Trust assumed shows that the Scout classifier assumes the partial demux functions are trusted. To supported untrusted demux functions, Scout would have to employ software fault-isolation [109] to sandbox the possibly malicious code. In contrast, the simple DPF filter are provably safe and hence can be supplied by untrusted users.
The third row, labelled Static size of code and data compares the static size of the code and data sections required by the two classifiers. This was measured by counting the number of bytes by which the size of test program increases when linking in one or the other classifier. In the DPF case, this includes the size of the vcode dynamic code generator, which accounts for about 74KB of the reported size [31].
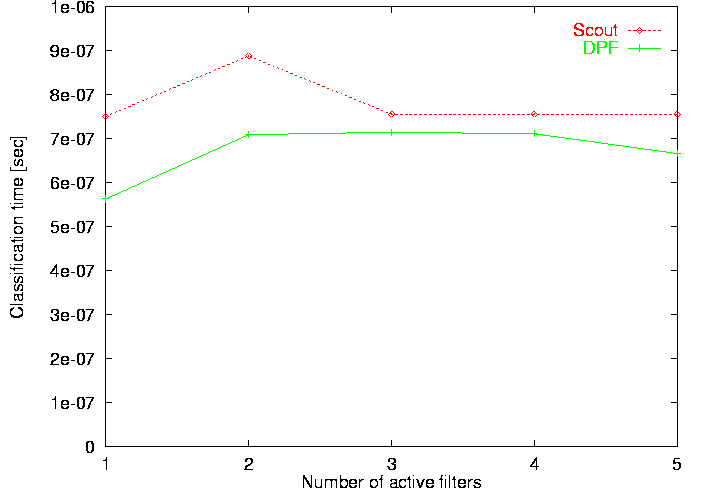
The next four rows lists various performance aspects. The row labelled Lookup active path lists the time required to classify a TCP/IP packet. To provide for a realistic environment, the classification was performed with three filters installed: one for the TCP/IP packets being looked up and one each for ARP and ICMP packets [79, 81]. The table shows that DPF is about 25% faster than the Scout classifier. This may sound like a large difference, but it corresponds to 62 CPU cycles which is marginal compared to the cost of fielding an interrupt, which can easily be several hundred cycles. The next row, labelled Lookup passive path, shows the 2N behavior of the Scout classifier discussed earlier. The data show that classifying a packet for a passive path is almost twice as expensive as for an active path. In contrast, DPF classification overhead increases by 16% only. Since passive paths are typically used to initiate path creation, the slower Scout time is not expected to significantly affect overall performance. It is also interesting to study classification performance as a function of the number of active TCP/IP filters in the classifier. This is illustrated in Figure 21. It shows that the Scout classification time remains largely unaffected by the number of active filters. The slightly larger time when two filters are active is a cache effect. DPF optimizes the case where just one filter is active, but uses a hash table for all other cases. Hence, classification time is slightly better with just one filter in place and remains largely constant when two or more filters are active. In Table 4, the rows labelled Insert passive path and Remove passive path show the time it takes to insert and remove a filter for a passive TCP/IP path. Insertion is more than six times slower for DPF than for Scout, which is due to the fact that DPF has to perform fairly sophisticated analysis of the newly inserted filter and because it requires dynamic code generation. It should be noted, however, that filter insertion/removal is typically less frequent than packet classification.
The last row, labelled Bytes per filter, shows the average size of the memory allocated dynamically per TCP/IP filter. In the Scout case, adding a TCP/IP filter requires just one demux node of 56 bytes if other TCP/IP filters are already installed. In the worst case, adding a TCP/IP filter to an empty classifier requires four demux nodes or 224 bytes. In contrast, DPF requires about 6-8KB per filter. This is because DPF uses a large, statically sized array to represent filters. Simple filters leave most of this array unused but, on the other hand, using a large array keeps the number of dynamic memory allocation requests to a minimum.
In summary, the comparison shows that the Scout classification approach is performance competitive with other classifiers and at the same time completely general. However, the above measurements should be considered optimistic, since the user-level test program makes some simplifying assumptions and since it assumes warm caches. For example, measurements with an actual Scout kernel indicate that, on an older 21064A Alpha clocked at 300MHz, classifying a TCP packet takes about 3.5µ when the instruction cache is warm, and about 7.2µs when the instruction cache is cold. In the warm-cache case, 0.8µs are spent on initializing and destroying the message data structure that Scout uses for the classification process, so the actual classification process takes 2.7µs. On the same machine, the test program reports a time of 1.14µs. This difference is most likely caused by three factors. First, the kernel implementation uses the normal Scout message abstraction instead of a simple linear byte sequence. Second, the kernel uses a more general and therefore more heavy-weight hash-table implementation and, third, the partial demultiplex functions are more widely scattered in the address space than in the test program. There is no reason these issues could not be addressed, but it is not clear whether doing so would result in an overall performance improvement that would make this worthwhile.