
This section uses the communication network analogy as a guide in developing a path model from first principles. The model is developed while largely ignoring the details of the various applications of paths that have been discussed on Chapter 1. This approach allows us to derive a path model without getting overwhelmed by the sometimes conflicting details of specific applications of paths. Once the path model has been developed, its usability is discussed and evaluated in Section 2.4 based on several sample applications.
Abstractly, a virtual circuit is a dataflow between two end-points. Thus, to a first approximation, we can model a path as a dataflow that starts at a source device and ends at a destination device. Since, respectively, the arrival and departure rates at the source and destination device may not always match with the rate at which data is processed by the path, the input and output devices are decoupled from the path by an input and output queue. These5 queues loosely correspond to the socket queues of a virtual circuit.
For paths to be general, arbitrary processing must be supported as part of moving data from the input to the output queue of a path. For example, if a path is used to receive a file on an Ethernet network adapter and save it to a disk, then the processing might involve TCP/IP and FTP protocol processing, as well as file system and SCSI related processing to save the file on disk. In essence, this processing would transform a sequence of network packets into a sequence of SCSI disk blocks. This arbitrary processing can be represented by a function g. If the input data (message) is m, then the output data deposited in the output queue is g(m). Note that this general processing in a path is in contrast to that of virtual circuits, where the processing function g is restricted to g(m)=m (ignoring packet losses and/or corruptions).

The basic path as discussed so far is illustrated in Figure 4. Devices are represented as circles; the path is shown in the center of the figure with its input and output queues, and the processing function g.
The input and output queues are needed to accommodate transients in the arrival and departure rates at the devices. However, the existence of those queues also implies that there is flexibility (within certain bounds) in choosing the time at which a data-item is moved from the path's input queue to its output queue. That is, the time at which g(m) is evaluated is under explicit control of a path scheduler. Path scheduling loosely corresponds to the queue service discipline used in the routers that are crossed by a virtual circuit.
Note that there is no one-to-one correspondence between paths and device-pairs. The same device-pair can be connected by zero, one, or several paths. Using multiple paths between the same device-pair may be sensible since either the g(m) or the scheduler may differ between the paths.
As alluded to earlier, the processing function g of a path can be arbitrarily complex. The question of what exactly determines g is best discussed with an example. Figure 5 repeats the modular system from Figure 3 but also shows a sample path as a bold line starting at module FDDI, passing through IP, UDP, MFLOW, MPEG, WiMP, and finally arriving at DISPLAY (for simplicity, the path queues are not shown).
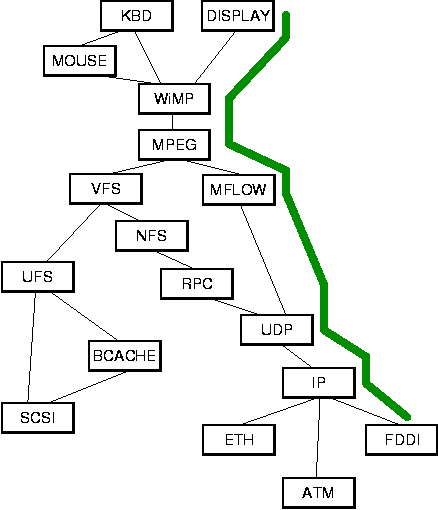
Presumably, each module processes data in a well-defined manner. For example, when receiving input data m, module IP might apply standard IP processing. This would result in output data gIP(m) which is the input data with the IP header stripped off. If we assume similar partial processing functions can be defined for the other modules along the path, then the processing that occurs along the path is equivalent to the composite of the application of the partial functions along the path:
Note that the right-hand side corresponds exactly to what would happen in a purely modular system without paths. An advantage of paths is that the sequence of partial functions is known and fixed once the path has been created. Using a semicolon (;) as the functional infix operator denoting function composition [66], the path processing function g can be expressed as:
This concisely demonstrates one of the fundamental benefits of paths:
they make it possible to express g independent of the input data
m. Among other things, this enables optimizing g by reducing or
simplifying the functional composite. For example, suppose g
consists of the composition g0;g1;g2;g3. If it turns out that
g2 is the inverse of function g1, then g can be reduced to
g0;g3.
Note that our functional approach to defining a path's semantics should not be mistaken to imply a particular implementation. It is certainly possible to realize the partial processing functions as individual procedures in a programming language such as C, but it would be equally legitimate to construct a path from a sequence of basic blocks, for example.
A critical missing piece of the path model defined so far is how and when paths are created. In many cases it is beneficial to exploit information that is available at runtime only. For this reason, paths need to be created and destroyed dynamically at runtime. For example, to distinguish between a video stream requiring realtime service and a video stream requiring best-effort service only, it is typically necessary to take some runtime information into account to be able to distinguish the two. If the video streams arrive over the network, then the port-number of the corresponding network connections may furnish this information.
The issue of how to create a path is rather interesting. There are two possible approaches:
Unfortunately, there are serious problems realizing this approach in practice. Pre-specifying a path often requires detailed knowledge of the internal workings of the modules encountered along a path. For example, whether the path in Figure 5 should go from IP to FDDI or to ATM will typically depend on the host that is sending the video and the routing information that is managed by the IP protocol. It certainly is imaginable to embed such detailed knowledge in the part of the system that would manage paths, but it is our contention that a much better solution is to follow the second approach, i.e., to create paths incrementally. With this approach, IP itself can make the decision whether or not the path should extend to ATM or FDDI.
Of course, when creating paths incrementally, there is the problem that path optimizations that depend on knowing the full path cannot be implemented this way. For this reason, incremental path creation must (in general) be followed by a second phase that takes the incrementally created path and transforms it into a globally optimized version. More on this later.
With these considerations in mind, we can now explain the path creation process in the proposed path model. When creating a path, it is first necessary to describe the kind of path that is desired. This description is in the form of name/value pairs. These pairs express information about the path that is guaranteed to remain true throughout the lifetime of the path. In other words, with respect to the lifetime of the path, these name/value pairs express invariants. In general, the more invariants are specified for a path, the better the quality of the path. This can be understood intuitively since we would expect that the more is known about a path, the easier it should be to create a well-optimized path.
Given a set of invariants, path creation is initiated at the module that is to form one end of the path. This module uses the invariants to make a routing decision, that is, a decision as to which module a path with the specified invariants must traverse next. Path creation is then forwarded to that next module. This process repeats itself until either there is no next module (i.e., the edge of the module graph has been reached) or until a module is reached that, based on the specified invariants, cannot make a definite routing decision. As part of making a routing decision, a module is free to update the invariants since new invariants may become available in that module or old invariants may be invalid beyond that module. Note that this does not contradict the requirement that invariants must hold true for the lifetime of the path. It simply means that there can be invariants that hold true only for a certain portion of a path.
An artifact of creating paths incrementally is that if the specified invariants are weak, the created path may be short. For example, with the module graph shown in Figure 5, UDP might create a path through IP specifying that any remote host is allowed to send packets to this path. In such a case, IP could not make a unique routing decision because packets could arrive through ETH, ATM, or FDDI. The resulting path would be short as it would go from UDP to IP only.
In the path model, paths therefore cannot be restricted to connecting device pairs. Instead, a path may connect any pair of modules. What are the implications of this? When a path is created, the creator expects a certain service from that path. That service must be rendered independent of whether the path happens to be short or long, although the quality or efficiency with which the service can be rendered may certainly be affected. In the previous example, IP would be responsible to ensure that packets for the short UDP-to-IP path are received independent of the remote host and it would also be responsible to forward such packets to the UDP-to-IP path. In other words, when a path terminates at a certain module, it is the responsibility of that module to ensure that data arriving on this path is continued to be processed appropriately. If the module is an interior module, this typically means that the module must make a dynamic routing decision that may lead to the data being forwarded to another (possibly also short) path. This case is illustrated in Figure 6. It depicts an interior module with a path that ends at this module and two paths that start at the module. When data arrives from the path above the module, it must make a dynamic routing decision to determined whether the data needs to be forwarded to the path at the lower left or the path at the lower right.

In the extreme case, a path may be so short that it simply connects a pair of neighboring modules. Of course, such degenerate paths do not help in avoiding the problems of purely modular systems, but the flip side of this coin is that the path model allows us to approximate a purely modular system with little extra complexity. In other words, for applications that are not performance sensitive and place no stringent demands on the quality of resource management they receive, it is possible to use short paths. This property also allows building prototypes quickly and optimize performance and behavior later, when the system is better understood.
One difficulty that remains with the previously described path creation scheme is that it forces path creation to start at the end of a path. This can be illustrated easily in our running example from Figure 5. Let us consider how a user might specify the playback of a video in the illustrated system. Most likely, the user would issue a command instructing playing the video located at, e.g., http://www.mpeg1.de/movies/maze.mpg on, for example, the graphics display of the machine (as opposed to saving the video to a local disk). Thus, one end of the path is implicitly determined by the address of the video server (http://www.mpeg1.de/) and the other end by the specification of the output device (the graphics display). The entity creating the path can and should specify the video source and output devices as path invariants, but it should not have to know how to translate those names into the modules that will terminate the path.

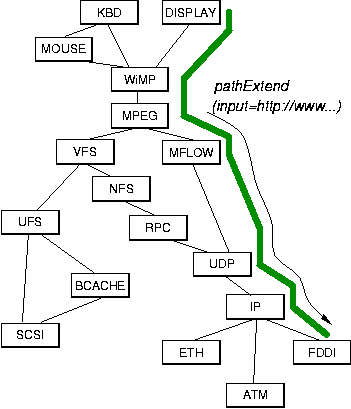
An elegant solution is to split up path creation: when a command is
received to display an MPEG encoded video, it is clearly necessary
that the path contains the MPEG module.
In such a scenario, there is not much point in applying global path optimizations right after creating a path that will be extended. Doing so would not cause incorrect behavior but it would most likely be wasteful. For this reason, it is best to keep global path optimization separate from path creation and extension. This also makes it possible to skip global path optimizations for paths that are not worth the added time or memory required to build an optimized path.
An alternative to path extension would be to first create two independent paths which are then combined at their common endpoint (at module MPEG, in the example). This solution was rejected since it would either necessitate transforming the identity of one path into that of the other or changing the path model to allow a hierarchical structure that can contain sub-paths. A change of identity might also necessitate moving resources reserved for one path to the other path, which is complex at best and impossible at worst. Hierarchical paths are undesirable as well since that would sacrifice the simple structure of paths. Both solutions would also suffer from the problem that a path combining operator would allow creation of nonsensical paths, such as circular paths. The path extension operator defined above suffers from none of these problems.
As explained earlier, paths are created incrementally, which results in maximum-length, though not necessarily optimal, paths. To obtain optimal paths, path transformations (optimizations) need to be applied in a second phase of path creation.
Abstractly, optimizing a path involves transformation rules which consist of <guard, transformation> pairs. If Path denotes the set of all possible paths, then the type signatures of the guard and the transformation functions are:
| guard: Path -> Boolean | |
| transformation: Path -> Path |
The idea of a transformation rule is that given a path p, guard(p) is first evaluated. If true, p is replaced by p'\getstransformation(p), otherwise, p'\gets p (i.e., the path is used unmodified). Since a path represents a maximum length sequence of modules and all other information pertinent to the operation of the path, transformation rules have as much context available as is possible. The quality of path optimization is therefore limited only by how long the path is (some paths may be shorter than one would like ideally) and by the quality of the transformation itself. Since it is applied at runtime, the amount of time available to the transformation is certainly bounded and in most cases limited to relatively short time-spans. Since the transformation needs to operate within a limited time budget, it is often advantageous to precompute expensive parts of the transformation off-line. Examples of such transformations will be discussed in Chapter 4.
A real system is expected to employ many path transformation rules. When multiple rules exist, they are applied repeatedly and in no particular order. The optimization phase stops when no rule can be found whose guard evaluates to true. Note that this is a conceptual model. An actual implementation would likely attempt to exploit the structure that may be present in the guards of the rules. For example, rather than evaluating guards linearly, it may be possible to build a decision tree that reduces the number of guards that need to be checked for a newly created path.
Invariants form the backbone of path creation and it is therefore worthwhile to discuss them in more detail. First, observe that invariants are essentially the vehicle that allows communicating information (knowledge) between modules. As such, the meaning of each name of an invariant must be universally agreed upon. Of course, each module does not have to know about all possible invariants, but it must be assured that if it uses an invariant of a given name, then every other module in the system must understand that invariant in the same way.
One question that arises is what a module should do if it encounters an invariant whose meaning it does not understand. It could either remove that invariant when passing on the path creation request, or it could leave it in the invariant set. The former is guaranteed to be safe, since it simply means that the path being constructed may end up being shorter than ideally would be the case. However, there are cases of important invariants that are known to be pervasive throughout the path. In such a case, it is desirable to tunnel such invariants through modules that do not understand their meaning. For this reason, two classes of invariants are defined: limited invariants that are removed when encountered by a module that does not understand them, and pervasive invariants that are passed through such modules unchanged. Finer-grained classifications are of course imaginable, but our experience is that this two-class scheme works well in practice.
At this point it may be helpful to discuss some concrete examples of invariants. Since invariants affect routing decisions, any kind of address information is typically specified as an invariant. For example, the path name of a datafile could be specified by an invariant named FILENAME. Similarly, the network address of a remote host that one wants to communicate with could be specified using an invariant called PARTICIPANT. Another kind of invariant that is often useful provides information about the data that will traverse the path. For example, if possible, it is often useful to specify a lower and upper bound on the size of a single data-item. Such an invariant obviously belongs to the class of limited invariants, since a module that does not understand this invariant may still change the size of any data-item passing through it. Thus, if the invariant were not limited, the module might unknowingly cause it to be violated. Data access patterns can also often be exploited, so specifying them as invariants is useful as well. For example, if a file is accessed in a strictly sequential fashion and its size is known, a cache module might be able to tell whether it is likely to be worthwhile to cache the file or whether it is better to leave the file uncached so other, already cached data does not get displaced. An example of a pervasive invariant may be one that indicates that the created path is intended to be used in a realtime environment. This property will be true independent of whether an intermediate module understands it or not.
This discussion should make it clear that there is a dependency between the invariants that can be usefully exploited and the invariants that can be specified. If the creator of a path does not know about the existence of some type of invariant, then it clearly cannot specify that invariant, even if it happens to be true for the path. Conversely, if a module does not know about the existence of an invariant, it cannot exploit it, even though it might be easy to do so if it had known about the invariant. Since it is not really possible to solve this dilemma perfectly, an iterative process seems appropriate. As will be discussed later on, Scout defines a (small) initial set of invariant names that are considered useful in exploiting various path benefits. As experience is collected and new means to exploit paths are invented, this set is bound to grow. This is unfortunate since it may require changing existing code to fully exploit new invariants (this is never required for correctness), but the hope is of course that this process will eventually converge on a manageable number and stable set of invariants.
The final question that needs to be answered with respect to path creation is: what is the entity that creates paths? In the path model we are proposing, this works as follows. When a system starts up, the constituent modules are initialized in some order. As part of its initialization, a module may elect to create one or more initial paths. After module initialization is complete, new paths may be created as a side effect of execution of other, already existing, paths. In other words, once the system is initialized, paths create paths.
For example, a networking service would typically create a path for its well-known address while its module is being initialized. Then, whenever it receives a new connection request, the service may elect to create a new path to handle the new connection. Similarly, a command-line interpreter is likely to create a path to the input device (e.g., the keyboard) during initialization. New paths are then created as a side-effect of handling key-strokes.
As defined so far, paths are simple and highly predictable: a data-item arrives at the input queue, the path is scheduled for execution, and the transformed data is deposited in the output queue. While this simplicity is ideal for the purpose of optimization, it also severely limits the usefulness of paths. It is thus necessary to extend paths to make them more widely applicable. The challenge is in doing this in a way that does not destroy the properties that make the path abstraction attractive in the first place.
Basic paths are essentially unidirectional dataflows. To be able to communicate in both directions (source to destination and vice versa), it would therefore be necessary to create two paths. This is a workable solution in many cases, but is not sufficient in others. In particular, for request-response like applications, it is typically necessary to guarantee that a reply returns along the exact same path through which the corresponding request arrived. Just as important, from the point of a user of a path, it is more convenient if the path used to send a request is also the one that will yield the reply.
In other cases, the two dataflow directions are mutually dependent. For example, in networking protocols it is often convenient and more efficient to piggy-back information about the state of the receiver on packets produced by the sender. If the two directions were handled by separate paths, it would be difficult, if not impossible, to communicate the necessary information from the receiver path to the sender path. As a final argument, consider resource consumption. Unidirectional paths consume less resources (memory, primarily) in a system where most paths are unidirectional, but they would use more resources in a system where many path pairs are needed to emulate bidirectional path. This argues neither for nor against bidirectional paths. However, it seems much easier to optimize bidirectional paths that are used in a unidirectional manner only than it would be to optimize a path-pair, since the latter consists of two independent entities. Based on this slight advantage and the other considerations that suggest bidirectional paths, it appears that extending the path model to support bidirectional dataflows is appropriate.
To support bidirectional dataflows, the path model can be extended as follows. Each extended path has four queues---an input and an output queue for each of the two directions. Also, the path function g is extended to take a second argument d that gives the direction (forward or backward) in which the path should be traversed. The module specific partial processing functions are extended analogously.
The reason the two directions are called forward and backward is that a path may wind its way up and down through a module graph. Thus, terms commonly used in layered systems, such as above and below or top and bottom are meaningless for paths. Forward and backward are more neutral terms but it is important to understand that these are just labels---the two directions are completely symmetric as far as the path model is concerned.
So far, the path model assumes that the path processing is work
conserving in the sense that for every input data-item, there is
exactly one output data-item.
For these reasons, it is necessary to loosen the evaluation rule for paths as follows. Suppose path processing consists of the composition of functions g1, ..., gn. With the new evaluation rule, a data-item may be injected at any one of these sub-functions and the invocation of gi may result either in gi-1 or in gi+1 being invoked. That is, these sub-functions can be invoked in any order, subject to the restriction that only neighboring functions are invoked, or that the data be enqueued at an output queue. Note that in the extreme, this allows for a data-item to loop endlessly inside a path. Of course, few, if any, useful paths would do this. However, the fact that the path model allows for endless looping is analogous to universal (Turing-complete) programming languages [24] which must allow for the possibility of infinite looping even though most useful programs terminate in a finite amount of time.