- Overview
-
Ergalics, the science of computer science, has as a primary goal the development of predictive causal models. Such models are a product of empirical sciences, with these sciences differentiated by what the models are about. For ergalics, the models make predictions about the behavior of computational tools, about the use of computational tools, and about computation itself.
For ergalics, spelling out predictive causal models is especially relevant because the discipline of computer science has historically relied on the mathematical and engineering perspectives, which utilize methodologies and formalisms different from that of the scientific perspective at issue here. So it is appropriate in this context to characterize these models. Interestingly, computer science, through the deep work of Judea Pearl and others, has contributed to our formal understanding of these models, by ascribing to the models' directed graph representation a precise semantics. The language of directed graphs is very familiar to computer scientists, rendering this language a useful entré into sophisticated empirical methods for representing hypotheses about relationships under study.
Predictive causal models relate independent variables (which can be manipulated) to dependent variables (which can be measured), generating predictions for the values of dependent variables given set values for the independent variables.
As a simple example, Newton's second law relates the impact of applying a force to an object (the force being an independent variable) to the velocity of an object (a dependent variable).
There have been many formal models that have been used to represent such relationships between independent and dependent variables, as well as methods for testing those relationships.
A SCM consists of a set of random variables (RVs) and the relationships between them. Each RV describes a particular aspect of the world as assuming, at any given time, one of some number of states or values. This set of values defines the domain of the RV, and the domain can be continuous or discrete. RVs may be observed (measured) or they may be posited to describe aspects of the world that cannot directly be observed (i.e., they are hidden or latent).
A RV also describes the tendency of the represented aspect of the world to assume particular values. This tendency is generally not considered in isolation: a central goal of the causal modeling framework is to represent the relationships between RVs. Such relationships determine how the value of a RV depends on the values of one or more other RVs.
Experimental control is a powerful tool for identifying whether observed dependencies between variables are due to direct causal relationship(s) or some other common cause.
There are a variety of modeling tools and resulting kinds of predictive causal models that one can construct. The discussion above has considered statistical methods, used heavily in other sciences as well. Other methods are relevant to ergalics, such as dynamical systems. At their core, all of these methods make claims about causal relationships among observed phenomena.
- DBMSes as a Domain of Ergalic Theories
-
As an example, let's consider database management systems (DBMSes) as a type of computational model for which we would like develop and test predictive causal models.
Despite their considerable engineering and the formal theory developed for them, DBMSes are not well understood. For example, there is surprisingly little known about the following, quite basic questions concerning the prevalent cost-based query optimization and two-phase locking transaction management architectures: (1) What is the relative impact of the non-linearity of some operator cost models on the selection of a suboptimal plan for a query? (2) How critical is the accuracy of the cost model in selecting good plans? (3) Does adding a physical operator for an algebraic operation always improve the effectiveness of query optimization, or is there a limit to the number of operators that can be practically a accommodated?
These questions get at the heart of research and development of DBMS query optimization, query evaluation, and transaction processing architectures and algorithms. They address fundamental limits and complex interactions within these architectures. But these questions share another commonality: they cannot be answered by investigating a single algorithm or even a single DBMS. Rather, they require the development of predictive models across multiple DBMSes.
Let's examine a causal structure that can address the third question above, concerning whether adding a physical operator always improves query optimization performance.
Query evaluation proceeds in several steps [Ramakrishnan 2003]. First, the query (generally expressed in SQL, a high-level declarative language) is translated into alternative query evaluation plans based on the relational algebra via query enumeration. The cost of each plan is then estimated and the plan with the lowest estimated cost is chosen. These steps comprise query optimization, specifically cost-based query optimization [Selinger 1979]. The identified query plan is then evaluated by the query execution engine which implements a set of physical operators, often several for each logical operator, such as join [Graefe 1993]
The third question above concerns the role of optimizer complexity, specifically, the number of physical operators that the optimizer must contend with, in relation to suboptimality, those situations when the optimizer selects the wrong plan, where there is another plan that is faster that the optimizer passed over. The goal is to determine if a fundamental limitation exists, which implies that it is necessary to study multiple instances of that optimization architecture. To do so, a model could be articulated for how and in what circumstances suboptimality arises and then evidence could be collected via hypothesis testing that this model can indeed predict the behavior of these several DBMSes.
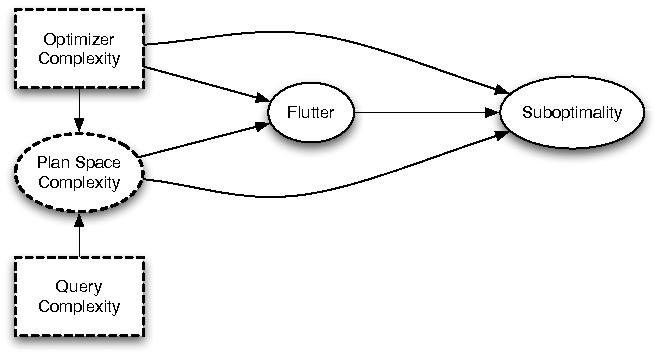 Figure 2: Model of relation between physical operators and suboptimality
Figure 2: Model of relation between physical operators and suboptimalityFigure 2 shows an example structural causal model hypothesizing the possible relationships between component phenomena in a database. The reasoning behind this model is that suboptimality is hypothesized to be due in part to the complexity of the optimizer and concomitant unanticipated interactions between the different components used within the optimizer. With the proliferation of concerns and variability that an optimizer must contend with, it is extremely difficult to ensure that for an arbitrary query that the optimizer will always pick the right plan. The components of the optimizer are all interacting with each other; this theory implicates these interactions as a primary source of suboptimality.
The central aspects of this model for the question at hand are the Optimizer Complexity variable and the causal paths from that variable to Suboptimality. The causal model states that if the optimizer is very complex, i.e., involving a large set of components that interact in complex ways, the optimizer will have a higher chance of fluttering as well as a higher chance of generating a suboptimal plan. This effect is due to four paths in the causal model: Optimizer Complexity can cause Suboptimality (i) directly, or (ii) by increasing the prevalence of flutter, which can cause suboptimality, or (iii) by increasing plan space complexity, which can directly cause suboptimality, or (iv) indirectly through flutter. Query Complexity also causes Suboptimality, but only indirectly, mediated by the Plan Space Complexity.
The next step is to develop hypotheses from the model that make predictions that can then be tested experimentally. Only if the model holds up to rigorous testing can it be used to address the question we started out with.
Analyses of experimental data over such predictive models also can indicate the relative strength of the causal paths in the model. For example, there are three causal paths impinging on Suboptimality in our model. Regression analysis of experimental data can estimate the amount of variance accounted for by each of these paths. Experiments can thus validate or refute intuition about what is really going on in these complex software systems, and can indicate the relative important of identified causal variables.
- Summary
-
Structural causal models allow predictions of the behavior of computational tools. Predictive models can make predictions about the tool itself, as the DBMS example above illustrates, or about the use of such tools, or about computation itself. A predictive model can be tested by comparing its predictions to what we observe in experiments. These tests give us evidence for whether the model accurately describes nature, lending credence to the model, and thus helping us uncover causal relationships. Knowing about these underlying causal relationship enables control of the computational tool, which then enables improvement (in terms of performance, functionality, reliability, and other engineering goals) as well as possibly mathematical insights in the form of new theorems.

