( See pdf version: pdf )
- Three Perspectives
-
Three quite distinct perspectives--mathematics, science, and engineering--have long been associated with the discipline of computer science. Mathematics appears in computer science (CS) through formalism, theories, and algorithms, which are ultimately mathematical objects that can be then expressed as computer programs and conversely. Engineering appears through our concern with making things better, faster, smaller, and cheaper. Science may be defined as developing general, predictive theories that describe and explain observed phenomena and evaluating these theories. Such theories include a statement of "why" and are amenable to predictions on heretofore unexamined phenomena, that can be subsequently tested on those phenomena [Davies 1973].
In an influential letter in the journal Science, Nobel Prize winner Herbert Simon and his colleagues Alan Newell and Alan Perlis defined the nascent discipline of CS as a "science of the artificial," strongly asserting that "the computer is not just an instrument but a phenomenon as well, requiring description and explanation" [Newell, Perlis, and Simon 1967]. Simon furthered that line of reasoning in his book, Sciences of the Artificial, whose third edition was published in 1996.
Simon's promise of a science of computational phenomena has not yet been realized by this fortieth anniversary of his compelling argument. Since its founding in the late 1950's, CS has uncovered deep mathematical truths and has constructed beautifully engineered systems that have ushered in the "age of information technology." However, there is as yet little understanding of these highly complex systems, what commonalities they share, how they can be used to construct new systems, why they interact in the ways they do with their environment, or what inherent limitations constrain them. As an example, while solid-state physics has provided a detailed understanding of VLSI, enabling design rules that allow the construction of highly complex processors, there is no similar understanding of the efficacy of programming language constructs and paradigms that would allow programming language designers to predict the efficiency of code written in their new languages. Nor do we have a detailed understanding of the failure modes of software components and systems assembled from those components, an understanding that would allow us to predict failure rates and to engineer systems to predictably decrease those rates.
The attainments of CS are largely the result of three contributing factors: the exponential growth of computing, storage, and communication capacity through Moore's Law; the brilliance of insightful designers; and the legions of programmers and testers that make these complex systems work by dint of sheer effort. Unfortunately, CS is now constrained in all three factors: the complexity of individual processors has leveled off, the systems are at the very edge of comprehension by even the most skilled architects, and the programming teams required for large systems now number in the thousands. Development "by hook or by crook" is simply not scalable, nor does it result in optimally effective systems. Specifically, unlike other engineering disciplines that have solid scientific foundations, CS currently has no way of knowing when a needed improvement can be attained through just pushing a technology harder, or whether a new technology is needed. Through a deeper understanding of computational tools and computation itself, our discipline can produce new tools that are more robust, more effective, and more closely aligned with the innate abilities and limitations of the developers and users.
CS has not yet achieved the structure and understanding that other sciences aspire to and to which the public ascribes the ascendancy of science. Consider as just one example how drugs now can be designed based on their desired shape, which was enabled by deep understanding of protein folding, chemical bonding, and biological pathways. This understanding is due primarily to the adoption of scientific reasoning. To achieve such understanding of computational tools and computation, the mathematical and engineering perspectives, while critical, are not sufficient. Rather, what is needed is the application of a radically different perspective, that of the scientific method, to enable and test scientific theories of computational artifacts.
Adopting the scientific perspective within CS, to augment the existing, vital perspectives of mathematics and engineering, requires that we seek a different understanding of computation, ask different questions, use different evaluative strategies, and interact in different ways with other disciplines.
- Seeking A Different Understanding
-
CS has been largely dominated by the engineering perspective. As a result of brilliant engineering, our discipline has generated a good number of industries, each revolving around stable, long-standing, complex, prevalently used computational tools. The engineering perspective can be characterized as seeking improvement, such as faster, more functional, more reliable.
CS has also successfully utilized the mathematical perspective. Complexity theory, asymptotic analysis, serializability theory, and other deep results have informed the study of computation in general and of the creation of software and hardware artifacts. The mathematical perspective can be characterized as seeking elegant formal structures and provable theorems within those structures.
The scientific perspective seeks a different kind of understanding: to explain phenomena encountered in nature. These explanations take the form of falsifiable scientific theories [Popper 1969] and scientific laws [Achinstein 1971]. The challenge to a scientist of any ilk is to reduce complex phenomena to simpler, measurable phenomena in such a way that the scientific community agrees that the essences of the original phenomena are captured. For example, Newton articulated the concept of "force" to explain the motion of the planets, John Nash provided an interpretation of human behavior as game playing, and E. O. Wilson and others dramatically changed ethology and ecology by introducing the ideas of energy budget and optimal foraging strategies.
The term "theory" in CS is a synonym for "formalism" or "concrete mathematics." When someone in CS does "theory," they are using the mathematical perspective. In logic, formal systems, and theorem proving, a "theory" is a purely formal object: a maximal set of assertions (strings) that can be deduced from axioms via inference rules. However, the term "theory" means something quite different in science.
Science seeks general, predictive theories that describe and explain observed phenomena. Such theories have four primary attributes.
- Parsimony: Each explains a variety of phenomena with a short, coherent explanation (Occam's razor), thereby reducing the number of independent phenomena.
- Generality: Each theory explains a wide range of phenomena.
- Prediction: Each anticipates future events, often to a high degree of accuracy.
- Explanatory power: Each provides a compelling underlying mechanism.
Successful theories are also highly useful in engineering, because they can be employed to design mechanisms that ensure positive effects or avoid negative effects.
To illustrate these benefits, consider one of the few extant scientific theories of computation, Peter Denning's Theory of Locality [Denning 2005b]. It is useful to examine this theory in order to understand specifically how a scientific theory is radically different from the theorems of the mathematical perspective and the architectures and design rules of the engineering perspective. The locality theory also illustrates why it is critical to take the creator and user into account.
The locality theory arose from a study of the cost of managing page transfers between main memory and a much slower disk drive. "Because a bad replacement algorithm could cost a million dollars of lost machine time over the life of a system," this was a critical problem to solve. Denning noticed when measuring the relevant phenomenon, the actual page usage of programs, that there were "many long phases with relatively small locality sets" (see Figure 1); "each program had its own distinctive pattern, like a voiceprint." He found that nothing about the structure of memory or the processor executing instructions required or forced such locality sets. Instead, it was a clear, repeated pattern across many systems, users, and programs. Denning abstracted this observed behavior as follows. Define D(x,t) as the distance from a processor to an object x at time t. If D(x,t) ≤ T for a specified distance threshold T, then x is defined to be in the locality set at time t. Locality theory states that if x is in the locality set at time t, then it is likely to be in the locality set at time t + δ, for small δ, and so should not be removed from the cache.
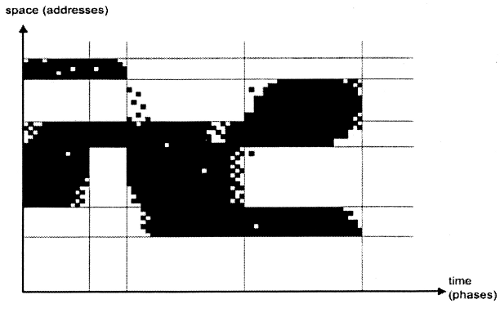Figure 1: Locality-sequence behavior during program execution ([Denning 2005b, page 23])The locality principle is inherently predictive and has been tested many, many times, for many distance functions. It is general: This theory applies to computational systems of all kinds: "in virtual memory to organize caches for address translation and to design the replacement algorithms, ... in buffers between computers and networks, ... in web browsers to hold recent web pages, ... in spread spectrum video streaming that bypasses network congestion" [Denning 2005b, pages 23-24].
Where the locality principle becomes a truly scientific theory is in its explanatory power. Specifically, this theory identifies the source of the observed locality. One might think that perhaps this observed phenomenon of a locality set comes about because of the von Neumann architecture. But locality was originally observed not at the level of the instruction set, but between the main memory and the disk. And as just mentioned, locality has been observed in contexts unrelated to the von Neumann architecture. Instead, locality appears to originate in the peculiar way in which humans organize information: This explanation by Denning of how locality works is reminiscent in some ways of Turing's explanation of his model of "machine," in which he appealed to how computing was done by (human) computers, an explanation which implicitly includes a notion of locality. "Computing is normally done by writing certain symbols on paper. We may suppose this paper is divided into squares like a child's arithmetic book. ... Besides ... changes of symbols, the ... operations must include changes of distribution of observed squares. The new observed squares must be immediately recognisable by the computer [a human computer--ed.]. I think it is reasonable to suppose that they can only be squares whose distance ... does not exceed a certain fixed amount." [Turing 1937, pages 249-50]. "The mind focuses on a small part of the sensory field and can work most quickly on the objects of its attention. People gather the most useful objects close around them to minimize the time and work of using them." Psychology has described this process in quite precise terms and with compelling theories of its own: the persistent steering of attention, the chunking and limited size of short-term memory, the serial processing of certain kinds of cognition. This realization, this scientific theory of locality, thus holds in many disparate contexts, and has enabled specific engineering advances, including register caching, virtual memory algorithms based on efficiently computing the working set, and buffer strategies within DBMSes and network routers, thereby increasing the performance, scalability, and reliability of many classes of computational tools.
The goal of ergalics is to express and test scientific theories of computational tools and of computation itself and thus to uncover general theories and laws that govern the behavior of these tools in various contexts. The challenge now before the CS discipline is to broaden its reliance upon the mathematical and engineering perspectives and to embrace the scientific perspective.
- The Subject of Ergalics: Computational Tools
-
The class of computational tools is broad and includes formalisms, conceptual devices, algorithms, languages, software systems, hardware, and computational infrastructure.
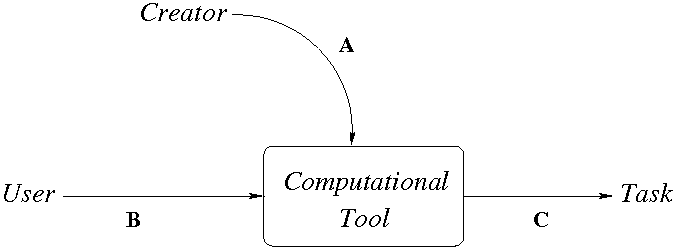Figure 2: Computational toolsExpanding on one of these categories, software systems include operating systems (e.g., Linux, Windows), database management systems (e.g., MySQL, Oracle), compilers and software development environments (e.g., Eclipse, gcc, Visual Studio), GUIs (e.g., Java Swing, Windows), internet servers (e.g., Apache, Internet Information Server), browsers (e.g., Internet Explorer, Mozilla Firefox), and network protocols (e.g., DNS, TCP/IP). Note that in each case there exist both open source systems and proprietary systems, that each system involves a highly functional and quite complex interface, and that each system has been around for at least a decade. Also note that each kind of software system is associated with an annual one billion US$ industry and that each each of the categories can be enumerated and expanded, for CS has produced many significant, long-standing, mature computational tools.
Figure 2 illustrates the range of phenomena to be investigated within ergalics and for which scientific theories can be advanced and tested. A computational tool is first created (arc A) by a person or team of people given an identified task. This tool is then used by a person (arc B) to accomplish that task (arc C). Phenomena can be associated with each arc. Most CS research considers how to create and compose tools that accomplish a specific task (arc C). Such research considers such aspects as functionality (what does the tool actually do?), performance (what resources, e.g., CPU execution time, disk and network bandwidth, cache, main memory, disk space, does the tool require?), and reliability (to what extent does the tool accommodate failures of the hardware and software components it utilizes?). For example, the problem Denning first considered in his doctoral dissertation that ultimately lead to his Theory of Locality was the performance implications of disk reads, specifically the phenomenon of thrashing.
The study of an individual tool, while potentially quite insightful, is however only a small portion of the phenomena that can be investigated and the insights that are possible. One could study how that tool was influenced by human traits. (We argued earlier that locality theory ultimately concerned exactly that.) Viewed another way, a computational tool is a means to bridge the computation gap between the abilities of the user and the requirements of the task. Hence, one could study how tools are actually used and their effectiveness in order to discover enduring predictions and theories about such use. (It is important to recognize that some systems may be sufficiently ad hoc that there may not be interesting scientific theories that can be applied to them. However, for established, long-lived computational tools such as those listed above, it is likely that there is much to be gleaned from careful scientific analysis.)
- Asking Different Questions
-
A focus on computational tools and on computation itself elicits a wide range of relevant research questions. Figure 3 expands on the relevant phenomena. In this figure, the arcs identify interactions and influences from one component to another, each suggesting some overarching research questions within ergalics. One can ask, which tasks are desired (arc D) and how does the task influence both the tool and the use of the tool? (One could even ask, can a tool developed for one task be applied for a perhaps quite different task?) Such questions get at the core of a "science of design".
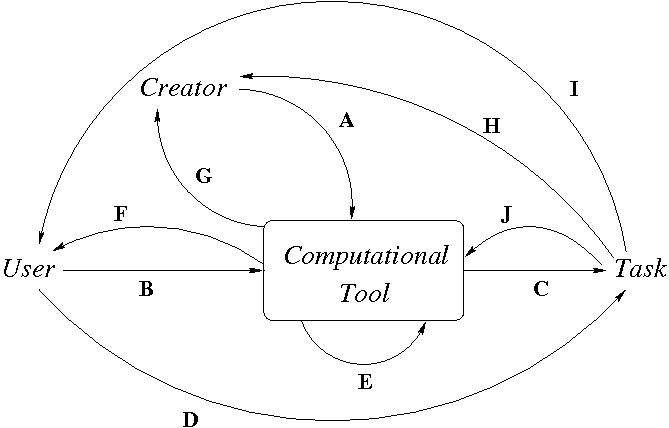Figure 3: Computational tools, elaboratedA defining characteristic of computational tools is their capability of creating other computational tools (arc E). For example, lex and yacc create parsers, graphical query tools create multipage SQL queries, and sophisticated hardware and software development environments produce code fragments or generate complete applications or hardware given higher-level specifications. How are the computational tools we create limited or impacted by those we have available today? Do tools created by other tools exhibit the same characteristics as tools created directly by humans? For example, compiler-generated assembly code looks very different from human-generated assembly code: the former tends to be more bloated. This is also true of machine-generated high-level code (many programming language implementations now compile down to the C programming language and then invoke gcc), to the point where machine-generated C programs are considered a good torture test for C compilers. Interestingly, such machine-generated code exhibits locality, in part because modern architectures make non-locality so punitively expensive that any reasonable programmer would be careful to pay attention to locality considerations.
CS has also very effectively exploited the generality of computational tools by leveraging abstraction: higher-level tools exploit the functionality of lower-level tools. The LAMP stack (Linux-Apache-MySQL-Perl) consists of over 10 million lines of code [Neville-Neil 2008]. This approaches the intellectual complexity of the Saturn V rocket that took man to the moon (with three million parts), but it is to date much less well understood. The LAMP stack is a testament to the brilliance and sheer brute force required in the absence of a scientific foundation. What are the underlying structuring principles, general and predictive theories, and inherent limitations of such complex assemblages of individual tools, each itself a complex assemblage of sophisticated modules?
The availability of computational tools can change the learning and work and play of its users (arc F) and creators (arc G); witness the facile, ubiquitous use of social networking and instant messaging by our youth. Carr asks, what is the internet doing to our brains? [Carr 2008]. Finally, tasks evolve, as new tools become available and as societal needs change, completing the social and cultural context within which the creator and user operate (arcs H and I) and thus indirectly impacting the evolution of tools and tool usage. Each of these arcs draws out an expansive range of phenomena to be studied, patterns to be identified, and the scientific theories to be uncovered as our understanding deepens.
As Newell, Perlis, and Simon emphasized, the science of computer science (ergalics) studies computational tools. Cohen agrees, "Unlike other scientists, who study chemical reactions, processes in cells, bridges under stress, animals in mazes, and so on, we study computer programs that perform tasks in environments." [Cohen 1995, page 2]. Whether studying a rat or a program, one must examine the behavior of the organism in context, as illustrated in Figure 4.
"Whether your subject is a rat or a computer program, the task of science is the same, to provide theories to answer three basic research questions:- How will a change in the agent's structure affect its behavior given a task and an environment?
- How will a change in an agent's task affect its behavior in a particular environment?
- How will a change in an agent's environment affect its behavior on a particular task?" [Cohen 1995, pages 3-4]
Note that the "organism" in Figure 4 is either the computational tool, with the user out of the picture or part of the environment, or the organism could be considered the user, with the computational tool being part of the environment, depending on which interaction of Figure 3 is under study.
A fourth basic research question is also relevant: How well does the agent perform the original task within the original environment? This can be viewed as another take on Figure 3.
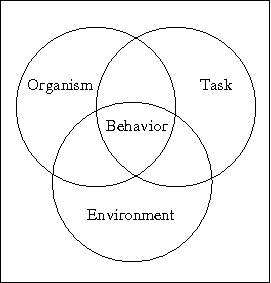Figure 4: How the structure, task, and environment of an organism influence its behavior ([Cohen 1995, page 3]) - Using Different Evaluative Strategies
-
The evaluative strategies used in other sciences suggest how we can evaluate our theories. Ergalics uses empirical generalization, in which understanding proceeds along two conceptual dimensions, as shown in Figure 5.
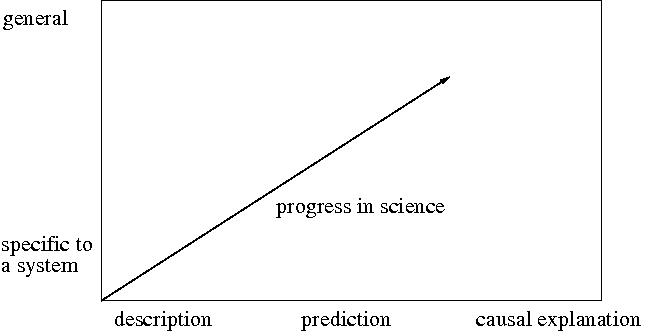Figure 5: Empirical generalization ([Cohen 1995, page 5])As Paul Cohen [Cohen 1995] has articulated, science (in general, and ergalics specifically) progresses (in the figure, on the y-axis) from studies of a particular system to statements about computational tools in general. So initial work might concern an aspect of a single program (e.g, a particular database query optimization algorithm in the context of a particular database management system), then generalize through studies of a class of systems (e.g., a study across several disparate DBMSs), to statements about computational tools in general (e.g., a theory that holds for rule-based optimizers, whether in DBMSs, AI systems, or compilers). This progression increases the domain of applicability, and thus the generality, of a theory.
Science (and ergalics) also progresses (in Figure 5, on the x-axis) from description of the phenomenon, to prediction, and eventually through causal explanation, within an articulated, thoroughly-tested theory. Such prediction and causal explanations involve statements about accessibility, applicability, composability, correctness, extendability, functionality, performance, reliability, robustness, scalability. usability, and utility. Deep understanding involves being able to accurately predict such aspects of a computational tool and to articulate compelling causal explanations as to why those predictions hold up.
While descriptions of how these tools work are available, there is little about extant computational tools that can be scientifically predicted and very little causal explanation. CS in its first fifty years has restricted itself largely to the bottom-left quadrant of this space. We propose to expand the perspective radically in both dimensions.
Science proceeds from a combination of induction from observed data and deduction from a stated theory. The initial theory construction phase starts from observation of phenomena to tentative hypotheses. The goal here is to develop a model of the world (that is, within the explicitly stated domain of applicability) that can yield predictions that are are tested against data drawn from measurements of that world (see Figure 6).
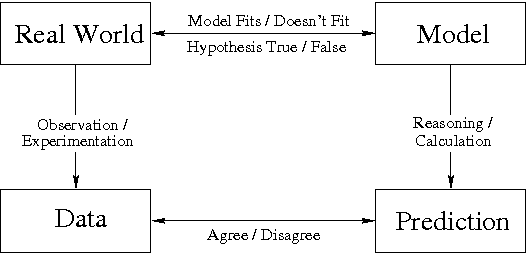Figure 6: Model Testing ([Giere 1979, page 30])The familiar process of debugging code can be viewed as an example of model testing. The real world consists of my program and its execution context: the compiler and the operating system and hardware on which the program runs. I test this program with some specified input data, as well as the specified correct output, which is what I hope the program will produce on this input data. I discover a flaw when the actual execution (the observation/experimentation) does not exactly correspond to the correct output. Through code inspection, I create my model: the line of code that I feel contains the flaw that produced the fault. I then form a prediction through reasoning or calculation: if I change that line of code, the regression test will now result in the expected output. My test of this hypothesis will tell me whether my model is an accurate reflection of (fits or doesn't fit) the world: does my prediction agree or disagree with the data actually produced when I reran the regression test? I could call this model a scientific theory, though it is not general at all (it applies only to this one program), it is not very predictive (it applies only to this one input data set), and it has weak explanatory power (it involves only the slice of the program involved in this regression test), thus placing this model towards the far bottom-left of Figure 5.
A scientific theory, its associated model, and predictions emanating from that model are tested until a more general theory emerges through insightful, creative induction. That theory is tested by deducing hypotheses, testing those hypotheses, and either confirming or rejecting them. Inevitably the theory is refined and its boundaries sharpened through further cycles of deductive testing and inductive refinement (* notes), as illustrated in Figure 7. This evolution of scientific theories occurs as a competition between competing models, with a range of evaluative tools to judge and select among them. The works of Ronald Giere [Giere 1979] and Paul Cohen [Cohen 1995] provide useful tools (methodological and analytical) to move up the empirical generalization arrow of Figure 5 and to compare the relative strength of competing theories.
From prediction comes control. Improvement in our computational tools derives from the predictive power of our scientific theories. Ultimately, the value to society of a specific ergalic theory derives from the extent to which that theory provides engineering opportunities for improvement of a class of computational tools and explains the inherent limitations of that class of tools. For example, Denning's theory initially enabled efficient virtual memory systems, at a time when such systems were ad hoc and at times inadequate. His insight allowed us to see how programmers can adjust their approach to take advantage of locality, by, for example, using new kinds of hardware and software architectures. His theory also explained why the lack of sufficient main memory to hold a process's working set would inevitably result in poor performance.
- Interacting with Other Disciplines in Different Ways
-
To this point CS primarily has offered computational tools and computational thinking to the other sciences, so that scientists in those domains can advance their own knowledge.
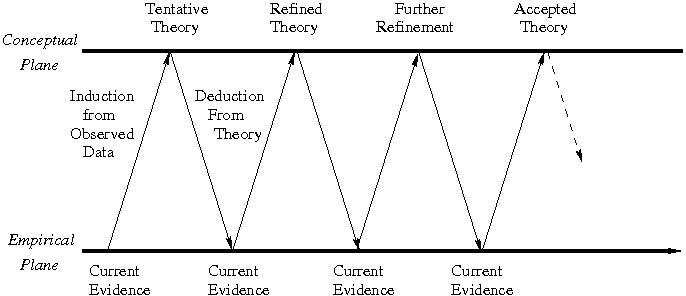Figure 7: Theory construction, testing, and refinement ([Kohli 2008])With ergalics, the flow can also go the other way: computer scientists can utilize the insights, methodologies, experimental strategies, formalisms, and extant theories of other sciences to aid our understanding of computational tools. Specifically, (i) psychology can contribute directly, through its understanding of the structures and limitations of cognitive and non-cognitive thinking and of the challenging but often insightful methodology of user studies; (ii) other behavioral and social sciences can also provide insights into the social implications of human use of computational tools, such as how the internet is used; (iii) neurology, through such tools as functional MRI, can start to identify physical brain structures that influence the creation and use of tools; (iv) economics and sociology can provide both micro and macro behavioral clues, such as how trust in security and privacy mechanisms may be attained, and (v) physics, chemistry, and biology can provide evidence of computational processes in nature and possible theories and laws about those processes, which would also govern the behavior of computational tools.
The models and theories these other fields have developed are all getting at the basic research questions that Cohen articulated, concerning animals, organizations, systems, and (in ergalics) computational tools. It is likely that the models will be more similar than different, because most arise from similar methodological tools and support the same kinds of inference: prediction, generalization, control, and, occasionally, causal explanation. Ergalics can do what these other sciences have done and are doing: utilize the empirical generalization of Figure 5 to ask the questions implied by Figure 4 and to follow the general approach of theory construction, testing, and refinement of Figure 7.
The fact that ergalics utilizes a common scientific terminology with shared semantics and a common research methodology can have another real benefit. Peter Lee, currently chair of Carnegie Mellon University's Department of Computer Science, asks, why is it that "there isn't much computing research in the major core-science publications" (Link). One possible reason is that CS does not as yet utilize the methodology and terminology of science, nor does it ask the questions of science, nor does it seek scientific theories. When CS participates in the market of enduring, technology-independent scientific theories (in this case, of computational tools), computing research may become more relevant for core-science publications.
- A New Direction
-
Ergalics seeks insights that are not based on details of the underlying technology, but rather continue to hold as technology inevitably and rapidly changes. It also seeks understanding of limitations on the construction and use of computational tools imposed by the nature of computation and by the specifics of human cognition. Ergalics provides an opportunity to apply new approaches, new methodological and analytical tools, and new forms of reasoning to the fundamental problems confronting CS and society in general. And it seeks to do so by bringing science into CS.
Science provides a specific methodology which has been extremely productive and beneficial in other sciences. The development of scientific theories in CS can produce new insights and better outcomes than restricting ourselves to the mathematical and engineering perspectives. Denning's recent assessment is hopeful, but as yet unrealized: "The science paradigm has not been part of the mainstream perception of computer science. But soon it will be" [Denning 2005a, page 31].
As Jeannette Wing stated in a talk at Stanford on May 21, 2008, the fundamental question of the Network Science and Engineering (NetSE) initiative is, "Is there a science for understanding the complexity of our networks such that we can engineer them to have predictable behavior?" (emphases in the original). Ergalics generalizes this challenge to computational tools and to computation itself, manifesting scientific theories across CS disciplines and enabling the engineering advances enabled by such theories. To achieve this result, we need to restructure the educational and scholarly ethos of CS to also encourage and enable the scientific perspective.
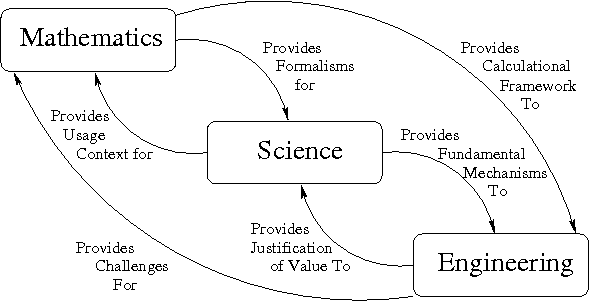Figure 8: The interrelationship of the three perspectivesBill Wulf has observed [Wulf 1995] that "Young as we [the discipline of CS] are, I think we really don't have a choice to be science or engineering; we are science and engineering, and something more, too." Figure 8 shows how the three perspectives, with science in the middle, symbiotically relate. Mathematics is often useful in providing formalisms to succinctly express theories (thus, aiding parsimony) and fit them in with other models of nature (generality). It also gives us a way to think about deep structure, and thus helps us to expose that structure. Science can be useful to engineering by explicating the underlying causal mechanisms (prediction and control). Similarly, engineering reveals behavior (phenomena) that science can use to construct new theories, and science provides needs for new formalisms and theorems.
As an example from aeronautics, the mathematics perspective has developed non-linear differential equations, in particular the Navier-Stokes equations, which can be used in the momentum equations for fluids such as air. The scientific perspective has used such formalisms to express thermodynamic laws, such as the perfect gas equation of state, relating pressure, density, and temperature. This physical theory allows one to accurately predict the viscous flow of a fluid around an object and the impact of changing temperature and pressure. The engineering perspective uses, for example, the Reynolds number, a notion grounded in these scientific laws, to scale data from wind tunnel experiments on wing shapes to their real-life counterparts.
This structure can be applied to CS, with concrete mathematics and complexity theory to the left, ergalics in the center, and most of conventional CS on the right.
- An Opportunity
-
People use computational tools. People also construct these tools. Computational tool construction and use is one of the ways that humans are unique. The tools that humans produce and the ways that they use such tools are profoundly affected by the way that humans think. Ultimately, understanding computational tools enables us to build better tools, and helps us to understand what makes us human.
Computation also appears to be a fundamental process in nature. If so, the scientific perspective affords a way to better understand our world.
Unlike established sciences, where many if not most of the fundamental theories have already been discovered (though much elaboration remains), the theories of ergalics are still out there, just waiting to be uncovered. Who will discover the CS equivalents of Einstein's theory of relativity, of Mendel's theory of heredity, of Darwin's theory of evolution, of Festinger's theory of cognitive dissonance, of Pauling's theory of chemical reactions? A grand adventure awaits us!
Webmaster: Andrey Kvochko